Giải đề thi học kì 2 toán lớp 10 năm 2019 - 2020 trường THPT Đống Đa - Hà Nội

Đề bài

Câu 1  (3,0 điểm):

Giải các bất phương trình sau:

a) \(\dfrac{{{x^2} - 3x + 2}}{{x + 2}} \ge 0\)

b) \(\left| {{x^2} - 5x + 5} \right| + 5 > 2x\)

c) \(\sqrt {7 - 2x}  < x + 4\)

Câu 2 (3,0 điểm):

a) Cho \(\cos a = \dfrac{5}{{13}}\) và \( - \dfrac{\pi }{2} < a < 0\). Tính các giá trị lượng giác còn lại của góc \(a\).

b) Rút gọn biểu thức sau (với giả thiết biểu thức có nghĩa)

\(A = \left( {\dfrac{{\sin x}}{{1 + \cos x}} + \dfrac{{1 + \cos x}}{{\sin x}}} \right)\cos x\)

Câu 3 (3,0 điểm):

Trong mặt phẳng tọa độ \(Oxy\), cho tam giác \(ABC\) có \(A\left( {1;2} \right),B\left( {3; - 4} \right)\) và đường thẳng chứa cạnh BC có phương trình \(2x - y - 10 = 0\).

a) Viết phương trình đường cao AH của tam giác ABC.

b) Viết phương trình đường tròn tâm A và tiếp xúc với cạnh BC.

c) Tìm tọa độ điểm C biết tam giác ABC cân tại C.

Câu 4 (1,0 điểm):

Tìm các giác trị của tham số \(m\) sao cho bất phương trình sau nghiệm đúng với mọi \(x \in \left[ {1;9} \right]\):

\({x^2} - 10x + 7\) \( + 2\sqrt { - {x^2} + 10x - 9}  + m > 0\)

Lời giải chi tiết

HƯỚNG DẪN GIẢI CHI TIẾT

Thực hiện: Ban chuyên môn

 Câu 1 (VD):

Phương pháp:

a) Xét dấu các nhị thức bậc nhất ở VT và suy ra tập nghiệm.

b) Sử dụng biến đổi tương đương: \(\left| f \right| > g \Leftrightarrow \left[ \begin{array}{l}f > g\\f <  - g\end{array} \right.\)

c) Sử dụng biến đổi tương đương \(\sqrt f  < g \Leftrightarrow \left\{ \begin{array}{l}g > 0\\0 \le f < {g^2}\end{array} \right.\)

Cách giải:

a) \(\dfrac{{{x^2} - 3x + 2}}{{x + 2}} \ge 0\)

ĐK: \(x + 2 \ne 0 \Leftrightarrow x \ne  - 2\)

Ta có:

\(\begin{array}{l}\dfrac{{{x^2} - 3x + 2}}{{x + 2}} \ge 0\\ \Leftrightarrow \dfrac{{\left( {x - 1} \right)\left( {x - 2} \right)}}{{x + 2}} \ge 0\end{array}\)

\(\begin{array}{l}x - 1 = 0 \Leftrightarrow x = 1\\x - 2 = 0 \Leftrightarrow x = 2\end{array}\)

Ta có bảng xét dấu:

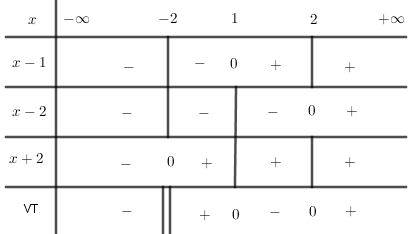
Từ bảng xét dấu suy ra \(S = \left( { - 2;1} \right] \cup \left[ {2; + \infty } \right)\).

b) \(\left| {{x^2} - 5x + 5} \right| + 5 > 2x\)

Ta có:

\(\begin{array}{l}\left| {{x^2} - 5x + 5} \right| + 5 > 2x\\ \Leftrightarrow \left| {{x^2} - 5x + 5} \right| > 2x - 5\\ \Leftrightarrow \left[ \begin{array}{l}{x^2} - 5x + 5 > 2x - 5\\{x^2} - 5x + 5 <  - \left( {2x - 5} \right)\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}{x^2} - 7x + 10 > 0\\{x^2} - 3x < 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x > 5\\x < 2\\0 < x < 3\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x < 3\\x > 5\end{array} \right.\end{array}\)

Vậy \(S = \left( { - \infty ;3} \right) \cup \left( {5; + \infty } \right)\).

c) \(\sqrt {7 - 2x}  < x + 4\)

\(\begin{array}{l}\sqrt {7 - 2x}  < x + 4\\ \Leftrightarrow \left\{ \begin{array}{l}x + 4 > 0\\0 \le 7 - 2x < {\left( {x + 4} \right)^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x + 4 > 0\\7 - 2x \ge 0\\7 - 2x < {\left( {x + 4} \right)^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x >  - 4\\x \le \dfrac{7}{2}\\7 - 2x < {x^2} + 8x + 16\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} - 4 < x \le \dfrac{7}{2}\\{x^2} + 10x + 9 < 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} - 4 < x \le \dfrac{7}{2}\\\left[ \begin{array}{l}x >  - 1\\x <  - 9\end{array} \right.\end{array} \right.\\ \Leftrightarrow  - 1 < x \le \dfrac{7}{2}\end{array}\)  

Vậy \(S = \left( { - 1;\dfrac{7}{2}} \right]\)

Câu 2 (VD):

Phương pháp:

a) Sử dụng công thức \({\sin ^2}a + {\cos ^2}a = 1\), kết hợp với điều kiện của \(a\) để tìm \(\sin a\).

Tù đó suy ra \(\tan a,\cot a\).

b) Quy đồng và rút gọn biểu thức, sử dụng đẳng thức \({\sin ^2}x + {\cos ^2}x = 1\)

Cách giải:

a) Cho \(\cos a = \dfrac{5}{{13}}\) và \( - \dfrac{\pi }{2} < a < 0\). Tính các giá trị lượng giác còn lại của góc \(a\).

Ta có: \({\sin ^2}a + {\cos ^2}a = 1\)

\(\begin{array}{l} \Rightarrow {\sin ^2}a + {\left( {\dfrac{5}{{13}}} \right)^2} = 1\\ \Rightarrow {\sin ^2}a = 1 - {\left( {\dfrac{5}{{13}}} \right)^2} = \dfrac{{144}}{{169}}\end{array}\)

Vì \( - \dfrac{\pi }{2} < a < 0\) nên \(a\) thuộc góc phần tư thứ IV \( \Rightarrow \sin a < 0\)

\(\begin{array}{l} \Rightarrow \sin a =  - \sqrt {\dfrac{{144}}{{169}}}  =  - \dfrac{{12}}{{13}}\\ \Rightarrow \tan a = \dfrac{{\sin a}}{{\cos a}}\\ =  - \dfrac{{12}}{{13}}:\dfrac{5}{{13}} =  - \dfrac{{12}}{5}\\ \Rightarrow \cot a = \dfrac{1}{{\tan a}}\\ = 1:\left( { - \dfrac{{12}}{5}} \right) =  - \dfrac{5}{{12}}\end{array}\)

Vậy \(\sin a =  - \dfrac{{12}}{{13}},\tan a =  - \dfrac{{12}}{5},\) \(\cot a =  - \dfrac{5}{{12}}\)

b) Rút gọn biểu thức sau (với giả thiết biểu thức có nghĩa)

\(\begin{array}{l}A = \left( {\dfrac{{\sin x}}{{1 + \cos x}} + \dfrac{{1 + \cos x}}{{\sin x}}} \right)\cos x\\ = \dfrac{{{{\sin }^2}x + {{\left( {1 + \cos x} \right)}^2}}}{{\sin x\left( {1 + \cos x} \right)}}.\cos x\\ = \dfrac{{{{\sin }^2}x + 1 + 2\cos x + {{\cos }^2}x}}{{\sin x\left( {1 + \cos x} \right)}}.\cos x\\ = \dfrac{{\left( {{{\sin }^2}x + {{\cos }^2}x} \right) + 1 + 2\cos x}}{{\sin x\left( {1 + \cos x} \right)}}.\cos x\\ = \dfrac{{1 + 1 + 2\cos x}}{{\sin x\left( {1 + \cos x} \right)}}.\cos x\\ = \dfrac{{2 + 2\cos x}}{{\sin x\left( {1 + \cos x} \right)}}.\cos x\\ = \dfrac{{2\left( {1 + \cos x} \right)}}{{\sin x\left( {1 + \cos x} \right)}}.\cos x\\ = \dfrac{{2\cos x}}{{\sin x}} = 2\cot x\end{array}\)

Bài 3 (VD):

Phương pháp:

a) Phương trình đường thẳng đi qua \(M\left( {{x_0};{y_0}} \right)\) và có VTPT \(\overrightarrow n  = \left( {a;b} \right)\) là \(a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) = 0\)

b) Phương trình đường tròn tâm \(I\left( {a;b} \right)\), bán kính \(R\) là \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}\)

c) Tam giác \(ABC\) cân tại \(C \Rightarrow CA = CB\) , kết hợp với điều kiện \(C\) thuộc đường thẳng \(BC\) ta tìm được tọa độ điểm \(C.\)

Cách giải:

Trong mặt phẳng tọa độ \(Oxy\), cho tam giác \(ABC\) có \(A\left( {1;2} \right),B\left( {3; - 4} \right)\) và đường thẳng chứa cạnh BC có phương trình \(2x - y - 10 = 0\).

a) Viết phương trình đường cao AH của tam giác ABC.

Đường thẳng \(BC\): \(2x - y - 10 = 0\) có 1 VTPT là \(\overrightarrow {{n_{BC}}}  = \left( {2; - 1} \right)\)

Vì \(AH \bot BC\) nên đường thẳng \(AH\) nhận  \(\overrightarrow {{n_{BC}}}  = \left( {2; - 1} \right)\) làm 1 VTCP

Suy ra \(\overrightarrow n  = \left( {1;2} \right)\) là 1 VTPT của đường thẳng \(AH\).

Đường thẳng AH đi qua \(A\left( {1;2} \right)\) và nhận \(\overrightarrow n  = \left( {1;2} \right)\) làm VTPT nên có phương trình:

\(1\left( {x - 1} \right) + 2\left( {y - 2} \right) = 0\) \( \Leftrightarrow x + 2y - 5 = 0\)

b) Viết phương trình đường tròn tâm A và tiếp xúc với cạnh BC.

Khoảng cách từ A đến đường thẳng BC là: \(d\left( {A;BC} \right) = \dfrac{{\left| {2.1 - 2 - 10} \right|}}{{\sqrt {{2^2} + {{\left( { - 1} \right)}^2}} }} = 2\sqrt 5 \)

Đường tròn tâm A tiếp xúc với cạnh BC nên có bán kính \(R = d\left( {A;BC} \right) = 2\sqrt 5 \)

Phương trình đường tròn cần tìm là: \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = {\left( {2\sqrt 5 } \right)^2}\)

\( \Leftrightarrow {\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 20\)

c) Tìm tọa độ điểm C biết tam giác ABC cân tại C.

Vì điểm C thuộc đường thẳng \(BC\): \(2x - y - 10 = 0\)\( \Leftrightarrow y = 2x - 10\) nên \(C\left( {x;2x - 10} \right)\)

\(AC = \sqrt {{{\left( {x - 1} \right)}^2} + {{\left( {2x - 12} \right)}^2}} \) và \(BC = \sqrt {{{\left( {x - 3} \right)}^2} + {{\left( {2x - 6} \right)}^2}} \)

Vì tam giác \(ABC\) cân tại \(C\) nên \(AC = BC\)

\( \Leftrightarrow \sqrt {{{\left( {x - 1} \right)}^2} + {{\left( {2x - 12} \right)}^2}} \) \( = \sqrt {{{\left( {x - 3} \right)}^2} + {{\left( {2x - 6} \right)}^2}} \)

\( \Leftrightarrow {\left( {x - 1} \right)^2} + {\left( {2x - 12} \right)^2}\) \( = {\left( {x - 3} \right)^2} + {\left( {2x - 6} \right)^2}\)

\( \Leftrightarrow {x^2} - 2x + 1 + 4{x^2} - 48x + 144\) \( = {x^2} - 6x + 9 + 4{x^2} - 24x + 36\)

\( \Leftrightarrow  - 50x + 145 =  - 30x + 45\)

\(\begin{array}{l} \Leftrightarrow 20x = 100\\ \Leftrightarrow x = 5\end{array}\)

Với \(x=5\) ta có: \(2.5-y-10=0\) hay \(y=0\).

Vậy \(C\left( {5;0} \right)\)

Bài 4 (VD):

Phương pháp:

Đặt \(\sqrt { - {x^2} + 10x - 9}  = t\left( {t \ge 0} \right)\) , tìm được \(0 \le t \le 4\)

Từ đó biện luận để đưa về dạng \(m > f\left( t \right)\), suy ra được giá trị của \(m\) theo điều kiện \(0 \le t \le 4\).

Cách giải:

Tìm các giác trị của tham số \(m\) sao cho bất phương trình sau nghiệm đúng với mọi \(x \in \left[ {1;9} \right]\):

\({x^2} - 10x + 7\) \( + 2\sqrt { - {x^2} + 10x - 9}  + m > 0\)  

Điều kiện: \( - 1 \le x \le 9\)

\({x^2} - 10x + 7\)\( + 2\sqrt { - {x^2} + 10x - 9}  + m > 0\)

\( \Leftrightarrow {x^2} - 10x + 9\)\( + 2\sqrt { - {x^2} + 10x - 9}  - 2 + m > 0\)

\( \Leftrightarrow  - \left( {{x^2} + 10x - 9} \right)\)\( + 2\sqrt { - {x^2} + 10x - 9}  - 2 + m > 0\)

Đặt \(\sqrt { - {x^2} + 10x - 9}  = t\) \(\left( {t \ge 0} \right)\), ta có bất phương trình

\(\begin{array}{l} - {t^2} + 2t - 2 + m > 0\\ \Leftrightarrow {t^2} - 2t + 2 - m < 0\\ \Leftrightarrow {\left( {t - 1} \right)^2} < m - 1\end{array}\)

Vì \(\sqrt { - {x^2} + 10x - 9}  \)\(= \sqrt {16 - {{\left( {x - 5} \right)}^2}}  \le 4\) nên với \(x \in \left[ {0;9} \right]\) thì \(t \in \left[ {0;4} \right]\)

Suy ra bất phương trình \({\left( {t - 1} \right)^2} < m - 1\) đúng với mọi \(t \in \left[ {0;4} \right]\)

Ta có: \(0 < t < 4 \Rightarrow t - 1 < 3\) \( \Leftrightarrow {\left( {t - 1} \right)^2} < 9\)

Suy ra \(m - 1 > 9 \Leftrightarrow m > 10.\)

Vậy \(m > 10\) thỏa mãn yêu cầu bài toán.