Giải đề thi học kì 1 toán lớp 11 năm 2019 - 2020 trường THPT Trần Phú

Câu 1. (1,5 đ) Giải phương trình lượng giác sau: \({\sin ^2}\left( {\dfrac{x}{2}} \right) - 2{\cos ^2}\left( {\dfrac{x}{4}} \right) + \dfrac{3}{4} = 0\).

Câu 2. (1đ)  Tìm số hạng không chứa \(x\) trong khai triển của biểu thức: \({\left( {3{x^3} - \dfrac{2}{{{x^2}}}} \right)^5}\).

Câu 3. (1đ)  Cho cấp số cộng \(\left( {{u_n}} \right)\) là một dãy số tăng thỏa mãn điều kiện \(\left\{ \begin{array}{l}{u_{31}} + {u_{34}} = 11\\u_{31}^2 + u_{34}^2 = 101\end{array} \right.\).

Tìm số hạng đầu tiên \({u_1}\), công sai \(d\) và số hạng tổng quát của cấp số cộng đó.

Câu 4. (1đ)  Một hộp có chứa \(4\) quả cầu màu đỏ, \(5\) quả cầu màu xanh và \(7\) quả cầu màu vàng. Lấy ngẫu nhiên cùng lúc ra \(4\) quả cầu từ hộp đó. Tính xác suất sao cho \(4\) quả cầu được lấy ra có đúng \(1\) quả cầu màu đỏ và không quá \(2\) quả cầu màu vàng.

Câu 5. (1đ) Cho một cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu tiên \({u_1} = 1\) và tổng \(100\) số hạng đầu bằng \(24850\). Tính \(S = \dfrac{1}{{{u_1}{u_2}}} + \dfrac{1}{{{u_2}{u_3}}} + \dfrac{1}{{{u_3}{u_4}}} + ...... + \dfrac{1}{{{u_{49}}{u_{50}}}}\).

Câu 6. (3đ) Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành tâm \(O\). Gọi \(G\) là trọng tâm của tam giác \(SAD\). Lấy điểm \(M\) thuộc cạnh \(AB\) sao cho \(AB = 3AM\).

1) Tìm giao tuyến của mặt phẳng \(\left( {SAD} \right)\) và mặt phẳng \(\left( {GBC} \right)\).

Tìm giao điểm \(H\) của đường thẳng \(BC\) với mặt phẳng \(\left( {SGM} \right)\).

2) Chứng minh rằng đường thẳng \(MG\) song song với mặt phẳng \(\left( {SBC} \right)\).

3) Mặt phẳng \(\left( \alpha  \right)\) đi qua \(M\) và song song với \(AD\) và \(SB\), \(\left( \alpha  \right)\) cắt các cạnh \(CD,\,\,SD,\,\,SA\) lần lượt tại các điểm \(N,\,\,P,\,\,Q\).

Xác định thiết diện của mặt phẳng \(\left( \alpha  \right)\) với hình chóp \(S.ABCD\).

Câu 7. (0,75 đ) Giải phương trình lượng giác sau: \(\dfrac{{\sin x + \sin 2x}}{{\sin 3x}} =  - 1\).

Câu 8. (0,75 đ) Từ các chữ số \(0;1;2;3;4;5;6;7;8;9\) có thể lập được tất cả bao nhiêu số tự nhiên chẵn có năm chữ số khác nhau và trong năm chữ số đó có đúng hai chữ số lẻ và hai chữ số lẻ này không đứng cạnh nhau.

HƯỚNG DẪN GIẢI CHI TIẾT

Thực hiện: Ban chuyên môn

Câu 1(VD): Giải phương trình lượng giác sau: \({\sin ^2}\left( {\dfrac{x}{2}} \right) - 2{\cos ^2}\left( {\dfrac{x}{4}} \right) + \dfrac{3}{4} = 0\).

Phương pháp

Sử dụng công thức hạ bậc \({\sin ^2}\alpha  = \dfrac{{1 - \cos 2\alpha }}{2};\) \({\cos ^2}\alpha  = \dfrac{{1 + \cos 2\alpha }}{2}\)

Cách giải:

\({\sin ^2}\left( {\dfrac{x}{2}} \right) - 2{\cos ^2}\left( {\dfrac{x}{4}} \right) + \dfrac{3}{4} = 0\)

\( \Leftrightarrow \dfrac{{1 - \cos x}}{2} - 2.\dfrac{{1 + \cos \dfrac{x}{2}}}{2} + \dfrac{3}{4} = 0\) \( \Leftrightarrow 2 - 2\cos x - 4 - 4\cos \dfrac{x}{2} + 3 = 0\)

\( \Leftrightarrow \left( {2\cos x - 1} \right) + 4\cos \dfrac{x}{2} = 0\) \( \Leftrightarrow {\cos ^2}\dfrac{x}{2} + 4\cos \dfrac{x}{2} = 0\) \( \Leftrightarrow \cos \dfrac{x}{2}\left( {\cos \dfrac{x}{2} + 4} \right) = 0\)

\( \Leftrightarrow \left[ \begin{array}{l}\cos \dfrac{x}{2} = 0\\\cos \dfrac{x}{2} + 4 = 0\left( {VN} \right)\end{array} \right.\) \( \Leftrightarrow \dfrac{x}{2} = \dfrac{\pi }{2} + k\pi \) \( \Leftrightarrow x = \pi  + k2\pi \)

Vậy phương trình có nghiệm \(x = \pi  + k2\pi \), \(k \in \mathbb{Z}\).

Câu 2(VD): Tìm số hạng không chứa \(x\) trong khai triển của biểu thức: \({\left( {3{x^3} - \dfrac{2}{{{x^2}}}} \right)^5}\).

Phương pháp

Sử dụng công thức tính số hạng tổng quát \({T_{k + 1}} = C_n^k{a^{n - k}}{b^k}\).

Cách giải:

Số hạng tổng quát : \({T_{k + 1}} = C_5^k.{\left( {3{x^3}} \right)^{5 - k}}.{\left( { - \dfrac{2}{{{x^2}}}} \right)^k}\) \( = C_5^k{.3^{5 - k}}.{x^{15 - 3k}}.\dfrac{{{{\left( { - 2} \right)}^k}}}{{{x^{2k}}}}\) \( = C_5^k{.3^{5 - k}}.{\left( { - 2} \right)^k}.{x^{15 - 5k}}\)

Số hạng không chứa \(x\) ứng với \(15 - 5k = 0 \Leftrightarrow k = 3\)

Vậy số hạng không chứa \(x\) là \(C_5^3{.3^{5 - 3}}.{\left( { - 2} \right)^3} =  - 720\).

Câu 3(VD): Cho cấp số cộng \(\left( {{u_n}} \right)\) là một dãy số tăng thỏa mãn điều kiện \(\left\{ \begin{array}{l}{u_{31}} + {u_{34}} = 11\\u_{31}^2 + u_{34}^2 = 101\end{array} \right.\).

Tìm số hạng đầu tiên \({u_1}\), công sai \(d\) và số hạng tổng quát của cấp số cộng đó.

Phương pháp

Sử dụng công thức: \({u_n} = {u_1} + \left( {n - 1} \right)d\).

Cách giải:

Ta có : \(\left\{ \begin{array}{l}{u_{31}} + {u_{34}} = 11\\u_{31}^2 + u_{34}^2 = 101\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{u_{34}} = 11 - {u_{31}}\\u_{31}^2 + {\left( {11 - {u_{31}}} \right)^2} = 101\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{u_{34}} = 11 - {u_{31}}\\2u_{31}^2 - 22{u_{31}} + 121 = 101\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}{u_{34}} = 11 - {u_{31}}\\2u_{31}^2 - 22{u_{31}} + 20 = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{u_{34}} = 11 - {u_{31}}\\{u_{31}} = 2,{u_{31}} = 10\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}{u_{31}} = 2,{u_{34}} = 9\\{u_{31}} = 10,{u_{34}} = 1\end{array} \right.\)

Mà dãy \(\left( {{u_n}} \right)\) tăng nên \({u_{34}} > {u_{31}}\), do đó \({u_{31}} = 2,{u_{34}} = 9\)

\( \Rightarrow \left\{ \begin{array}{l}{u_1} + 30d = 2\\{u_1} + 33d = 9\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}d = \dfrac{7}{3}\\{u_1} =  - 68\end{array} \right.\)

Số hạng tổng quát \({u_n} =  - 68 + \dfrac{7}{3}\left( {n - 1} \right)\).

Vậy \({u_1} =  - 68,d = \dfrac{7}{3},\)\({u_n} =  - 68 + \dfrac{7}{3}\left( {n - 1} \right)\).

Câu 4(VD): Một hộp có chứa \(4\) quả cầu màu đỏ, \(5\) quả cầu màu xanh và \(7\) quả cầu màu vàng. Lấy ngẫu nhiên cùng lúc ra \(4\) quả cầu từ hộp đó. Tính xác suất sao cho \(4\) quả cầu được lấy ra có đúng \(1\) quả cầu màu đỏ và không quá \(2\) quả cầu màu vàng.

Phương pháp

- Tính số phần tử không gian mẫu \(n\left( \Omega  \right)\)

- Tính số khả năng có lợi cho biến cố \(A\) đã cho.

- Tính xác suất \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega  \right)}}\).

Cách giải:

Chọn \(4\) trong \(16\) quả cầu, \(n\left( \Omega  \right) = C_{16}^4 = 1820\).

Gọi \(A\) là biến cố: “Có đúng \(1\) quả cầu đỏ và không quá \(2\) quả cầu vàng”

TH1: Chọn được \(1\) quả cầu đỏ, \(2\) quả cầu vàng, \(1\) quả cầu xanh có \(C_4^1.C_7^2.C_5^1 = 420\) cách.

TH2: Chọn được \(1\) quả cầu đỏ, \(1\) quả cầu vàng, \(2\) quả cầu xanh có \(C_4^1.C_7^1.C_5^2 = 280\) cách.

TH3: Chọn được \(1\) quả cầu đỏ, \(0\) quả cầu vàng, \(3\) quả cầu xanh có \(C_4^1.C_7^0.C_5^3 = 40\) cách.

Do đó \(n\left( A \right) = 420 + 280 + 40 = 740\).

Xác suất \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega  \right)}} = \dfrac{{740}}{{1820}} = \dfrac{{37}}{{91}}\).

Câu 5(VD): Cho một cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu tiên \({u_1} = 1\) và tổng \(100\) số hạng đầu bằng \(24850\). Tính \(S = \dfrac{1}{{{u_1}{u_2}}} + \dfrac{1}{{{u_2}{u_3}}} + \dfrac{1}{{{u_3}{u_4}}} + ...... + \dfrac{1}{{{u_{49}}{u_{50}}}}\).

Phương pháp

- Tìm CSC đã cho bằng cách sử dụng công thức \({S_n} = \dfrac{{n\left[ {2{u_1} + \left( {n - 1} \right)d} \right]}}{2}\)

- Thay vào tổng đã cho tính toán.

Cách giải:

Ta có : \(24850 = {S_{100}} = \dfrac{{100\left( {2.1 + 99d} \right)}}{2}\)\( \Leftrightarrow d = 5\)

Khi đó \({u_1} = 1,{u_2} = 6,{u_3} = 11,{u_4} = 16,...\) \({u_{49}} = {u_1} + 48d = 241\), \({u_{50}} = {u_1} + 49d = 246\)

\( \Rightarrow S = \dfrac{1}{{{u_1}{u_2}}} + \dfrac{1}{{{u_2}{u_3}}} + ... + \dfrac{1}{{{u_{49}}.{u_{50}}}}\) \( = \dfrac{1}{{1.6}} + \dfrac{1}{{6.11}} + \dfrac{1}{{11.16}} + ... + \dfrac{1}{{241.246}}\)

\( = \dfrac{1}{5}\left( {\dfrac{1}{1} - \dfrac{1}{6}} \right) + \dfrac{1}{5}\left( {\dfrac{1}{6} - \dfrac{1}{{11}}} \right) + \) \(... + \dfrac{1}{5}\left( {\dfrac{1}{{241}} - \dfrac{1}{{246}}} \right)\)

\( = \dfrac{1}{5}\left( {1 - \dfrac{1}{6} + \dfrac{1}{6} - \dfrac{1}{{11}} + ... + \dfrac{1}{{241}} - \dfrac{1}{{246}}} \right)\)

\( = \dfrac{1}{5}\left( {1 - \dfrac{1}{{246}}} \right) = \dfrac{{49}}{{246}}\)

Vậy \(S = \dfrac{{49}}{{246}}\).

Câu 6(VD): Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành tâm \(O\). Gọi \(G\) là trọng tâm của tam giác \(SAD\). Lấy điểm \(M\) thuộc cạnh \(AB\) sao cho \(AB = 3AM\).

Phương pháp

a) Sử dụng định lí ba giao tuyến song song: \(\left\{ \begin{array}{l}\left( \alpha  \right) \cap \left( \beta  \right) = {d_1}\\\left( \beta  \right) \cap \left( \gamma  \right) = {d_2}\\\left( \alpha  \right) \cap \left( \gamma  \right) = {d_3}\\{d_1}//{d_2}\end{array} \right. \Rightarrow {d_3}//{d_1}//{d_2}\).

b) Sử dụng định lí \(\left\{ \begin{array}{l}a \not\subset \left( P \right)\\a//b\\b \subset \left( P \right)\end{array} \right. \Rightarrow a//\left( P \right)\).

c) Sử dụng hệ quả \(\left\{ \begin{array}{l}a//\left( P \right)\\a \subset \left( Q \right)\\\left( P \right) \cap \left( Q \right) = d\end{array} \right. \Rightarrow a//d\).

Cách giải:

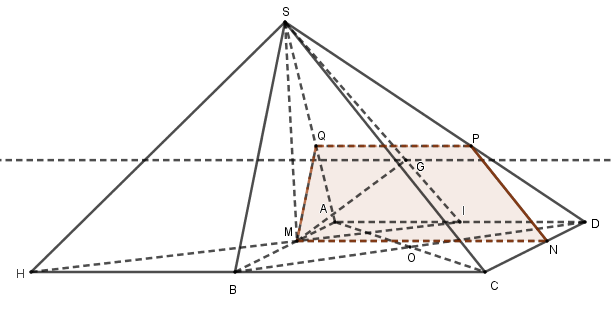
1) Tìm giao tuyến của mặt phẳng \(\left( {SAD} \right)\) và mặt phẳng \(\left( {GBC} \right)\). Tìm giao điểm \(H\) của đường thẳng \(BC\) với mặt phẳng \(\left( {SGM} \right)\).

Dễ thấy \(G \in \left( {GBC} \right) \cap \left( {SAD} \right)\).

Xét các mặt phẳng: \(\left( {GBC} \right),\left( {SAD} \right),\left( {ABCD} \right)\) có:

\(\left\{ \begin{array}{l}\left( {GBC} \right) \cap \left( {SAD} \right) = Gx\\\left( {SAD} \right) \cap \left( {ABCD} \right) = AD\\\left( {ABCD} \right) \cap \left( {GBC} \right) = BC\\BC//AD\end{array} \right.\) \( \Rightarrow Gx//AB//CD\)

Vậy \(\left( {SAD} \right) \cap \left( {GBC} \right) = Gx\) là đường thẳng đi qua \(G\) và song song \(AD\).

Gọi \(I\) là trung điểm \(AD\), khi đó \(\left( {SGM} \right) \equiv \left( {SIM} \right)\).

Trong \(\left( {ABCD} \right)\), gọi \(H = IM \cap BC\) \( \Rightarrow \left\{ \begin{array}{l}H \in IM \subset \left( {SIM} \right)\\H \in BC\end{array} \right.\) \( \Rightarrow H = BC \cap \left( {SMG} \right)\).

2) Chứng minh rằng đường thẳng \(MG\) song song với mặt phẳng \(\left( {SBC} \right)\)

Vì \(AD//BC\) nên \(\dfrac{{MI}}{{MH}} = \dfrac{{MA}}{{MB}} = \dfrac{1}{2}\)

Xét tam giác \(SIH\) có \(\dfrac{{MI}}{{MH}} = \dfrac{{GI}}{{GS}} = \dfrac{1}{2}\) nên theo định lí Talet ta có \(MG//SH\).

Mà \(SH \subset \left( {SBC} \right)\) nên \(MG//\left( {SBC} \right)\).

3) Mặt phẳng \(\left( \alpha  \right)\) đi qua \(M\) và song song với \(AD\) và \(SB\), \(\left( \alpha  \right)\) cắt các cạnh \(CD,\,\,SD,\,\,SA\) lần lượt tại các điểm \(N,\,\,P,\,\,Q\). Xác định thiết diện của mặt phẳng \(\left( \alpha  \right)\) với hình chóp \(S.ABCD\).

Ta có:

\(\left\{ \begin{array}{l}SB//\left( \alpha  \right)\\SB \subset \left( {SAB} \right)\\\left( \alpha  \right) \cap \left( {SAB} \right) = MQ\end{array} \right.\) \( \Rightarrow MQ//SB\)

\( \Rightarrow \) Trong \(\left( {SAB} \right)\), kẻ \(Mx//SB\) cắt \(SA\) tại \(Q\).

\(\left\{ \begin{array}{l}AD//\left( \alpha  \right)\\AD \subset \left( {SAD} \right)\\\left( \alpha  \right) \cap \left( {SAD} \right) = QP\end{array} \right.\) \( \Rightarrow QP//AD\)

\( \Rightarrow \) Trong \(\left( {SAD} \right)\), kẻ \(Qy//AD\) cắt \(SD\) tại \(P\).

\(\left\{ \begin{array}{l}AD//\left( \alpha  \right)\\AD \subset \left( {ABCD} \right)\\\left( \alpha  \right) \cap \left( {ABCD} \right) = MN\end{array} \right.\) \( \Rightarrow MN//AD\)

\( \Rightarrow \) Trong \(\left( {ABCD} \right)\), kẻ \(Mt//AD\) cắt \(CD\) tại \(N\).

Khi đó

\(\begin{array}{l}\left( \alpha  \right) \cap \left( {SAB} \right) = MQ\\\left( \alpha  \right) \cap \left( {SAD} \right) = QP\\\left( \alpha  \right) \cap \left( {SCD} \right) = PN\\\left( \alpha  \right) \cap \left( {ABCD} \right) = NM\end{array}\)

\( \Rightarrow \) Thiết diện là tứ giác \(MNPQ\).

Câu 7(VD): Giải phương trình lượng giác sau: \(\dfrac{{\sin x + \sin 2x}}{{\sin 3x}} =  - 1\).

Phương pháp

- Sử dụng công thức cộng \(\sin a + \sin b = 2\sin \dfrac{{a + b}}{2}\cos \dfrac{{a - b}}{2}\) biến đổi phương trình về dạng tích.

- Giải phương trình và đối chiếu điều kiện, kết luận nghiệm.

Cách giải:

ĐK: \(\sin 3x \ne 0 \Leftrightarrow 3x \ne k\pi \) \( \Leftrightarrow x \ne \dfrac{{k\pi }}{3}\)

PT\( \Rightarrow \sin x + \sin 2x =  - \sin 3x\) \( \Leftrightarrow \left( {\sin x + \sin 3x} \right) + \sin 2x = 0\)

\( \Leftrightarrow 2\sin 2x\cos x + \sin 2x = 0\) \( \Leftrightarrow \sin 2x\left( {2\cos x + 1} \right) = 0\)

\( \Leftrightarrow \left[ \begin{array}{l}\sin 2x = 0\\2\cos x + 1 = 0\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}\sin 2x = 0\\\cos x =  - \dfrac{1}{2}\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}2x = k\pi \\x =  \pm \dfrac{\pi }{3} + k2\pi \end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{k\pi }}{2}\\x =  \pm \dfrac{\pi }{3} + k2\pi \end{array} \right.,k \in \mathbb{Z}\)

Biểu diễn các nghiệm trên đường tròn lượng giác ta được:

 

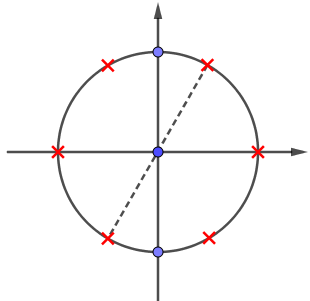
Quan sát hình vẽ ta thấy phương trình có nghiệm \(x = \dfrac{\pi }{2} + k\pi \), \(k \in \mathbb{Z}\) (hai điểm màu xanh).

Câu 8(VD): Từ các chữ số \(0;1;2;3;4;5;6;7;8;9\) có thể lập được tất cả bao nhiêu số tự nhiên chẵn có năm chữ số khác nhau và trong năm chữ số đó có đúng hai chữ số lẻ và hai chữ số lẻ này không đứng cạnh nhau.

Phương pháp

- Đếm các số chẵn có \(5\) chữ số khác nhau mà có đúng hai chữ số lẻ.

- Đếm các số chẵn có \(5\) chữ số khác nhau mà có hai chữ số lẻ đứng cạnh nhau.

- Trừ các kết quả cho nhau ta dược đáp số.

Cách giải:

Gọi số có năm chữ số có dạng \(\overline {abcde} \).

TH1: \(e = 0\) có \(1\) cách chọn.

Chọn \(2\) chữ số lẻ và \(2\) chữ số chẵn và xếp vị trí cho chúng có \(C_5^2.C_4^2.4!\) cách chọn.

Do đó có  \(C_5^2.C_4^2.4!\) số.

TH2: \(e \in \left\{ {2;4;6;8} \right\}\) có \(4\) cách chọn.

+) Nếu \(a\) chẵn, \(a \ne 0,a \ne e\) thì có \(3\) cách chọn.

Số cách chọn 3 chữ số còn lại (\(1\) chữ số chẵn và \(2\) chữ số lẻ) và xếp vị trí cho chúng là \(C_3^1.C_5^2.3!\) cách chọn.

Do đó có \(3.C_3^1.C_5^2.3!\) số.

+) Nếu \(a\) lẻ thì có \(5\) cách chọn.

Số cách chọn 3 chữ số còn lại (\(2\) chữ số chẵn và \(1\) chữ số lẻ) và xếp vị trí cho chúng là \(C_4^2.C_4^1.3!\) cách chọn.

Do đó có \(5.C_4^2.C_4^1.3!\) số.

Khi đó số các số chẵn có \(5\) chữ số khác nhau mà chỉ có đúng \(2\) chữ số lẻ là \(C_5^2.C_4^2.4! + 4.\left( {3.C_3^1.C_5^2.3! + 5.C_4^2.C_4^1.3!} \right) = 6480\) số.

Ta tính số các số chẵn có \(5\) chữ số khác nhau chỉ có \(2\) chữ số lẻ mà chúng đứng cạnh nhau.

Coi hai chữ số lẻ đứng cạnh nhau là một chữ số \(A\), có \(A_5^2\) cách chọn và sắp xếp vị trí của hai chữ số trong \(A\).

Số có dạng \(\overline {abcd} \) với \(a,b,c,d \in \left\{ {A;0;2;4;6;8} \right\}\).

+) Nếu \(a = A\) thì có \(A_5^3\) cách chọn \(b,c,d\).

+) Nếu \(a \ne A,a \ne 0\) thì có \(4\) cách chọn.

\(A\) có thể đứng ở vị trí \(b\) hoặc \(c\) nên có \(2\) cách xếp.

Có \(A_4^2\) cách chọn và sắp xếp hai chữ số còn lại.

Do đó có \(A_5^2\left( {A_5^3 + 4.2.A_4^2} \right) = 3120\)

Vậy có \(6480 - 3120 = 3360\) số.