Giải đề thi học kì 1 toán lớp 11 năm 2019 - 2020 trường THPT chuyên Trần Đại Nghĩa

A. PHẦN CHUNG (6 điểm)

Bài 1 (1 điểm):

Giải phương trình: \(4\sin x\cos x + 2\sin x - 2\sqrt 3 \cos x - \sqrt 3  = 0.\)

Bài 2 (VD) (1 điểm):

Xác định hệ số của số hạng không chứa \(x\) trong khai triển \({\left( {{x^3} - \dfrac{3}{x}} \right)^8}.\)

Bài 3 (1 điểm):

Ba xạ thủ bắn vào bia một cách độc lập, mỗi người bắt một viên đạn. Xác suất bắn trúng của ba xạ thủ lần lượt là 0,5; 0,6 và 0,8. Tính xác suất để có ít nhất hai người bắn trúng đích.

Bài 4 (1 điểm):

Bạn Bình muốn mua một món quà trị giá 900.000 đồng để tặng mẹ nhân ngày sinh nhật của mẹ vào ngày 30/9/2019. Bạn bỏ ống heo tiết kiệm mỗi ngày một lần, bắt đầu từ ngày 01/08/2019 cho đến ngày sinh nhật của mẹ. Theo cách: lần đầu tiên bỏ ống heo 500 đồng, sau đó cứ lần sau bỏ nhiều hơn lần trước 500 đồng. Hỏi đến sinh nhật mẹ Bình có đủ tiền mua quà không?

Bài 5 (2 điểm):

Cho hình chóp \(SABCD\) có đáy là hình bình hành tâm \(O.\) Gọi \(E,\,\,H,\,\,F\) lần lượt là trung điểm của \(AD,\,\,DC,\,\,CB.\)

1) Gọi \(I\) là trung điểm của \(SF.\) Chứng minh \(IO\) song song với mặt phẳng \(\left( {SAD} \right).\)

2) Gọi \(G,\,\,K\) lần lượt là trọng tâm của \(\Delta SAD,\,\,\Delta SCD,\,\,M\) là trung điểm của \(IF.\) Chứng minh rằng mặt phẳng \(\left( {GKI} \right)\) song song với mặt phẳng \(\left( {EHM} \right).\) 

B. PHẦN RIÊNG (4 điểm)

I. Dành cho lớp 11A1, 11A2, 11CL, 11CH, HCS.

Bài 5a (1,5 điểm) (Làm tiếp bài 5):

Gọi \(\left( P \right)\) là mặt phẳng chứa \(EH\) và song song với \(IG.\) Xác định thiết diện của mặt phẳng \(\left( P \right)\) với hình chóp \(SABCD.\)

Bài 6a (1 điểm):

Xét tính tăng, giảm cũa dãy số \({\left( u \right)_n}\) với \({u_n} = \dfrac{n}{{{n^2} + 1}}.\)

Bài 7a (1,5 điểm):

Vòng chung kết của một giải đấu bóng đá ở châu Á có 16 đội tuyển tham gia được chia vào 4 Nhóm (như bảng bên dưới).

Ban tổ chức bốc thăm để chia 16 đội này vào 4 bảng A, B, C, D sao cho trong mỗi bảng, không có hai đội nào ở cùng Nhóm (nghĩa là mỗi Bảng phải có đủ: Một đội của Nhóm 1, một đội của Nhóm 2, một đội của Nhóm 3, một đội của Nhóm 4).

Tính xác suất của biến cố: ‘‘Không có bảng nào có nhiều hơn một đội của khu vực Đông Nam Á’’.

II. Dành cho lớp 11CA1, 11CA2, 11CA3, 11CV

Bài 5b (1,5 điểm) (Làm tiếp bài 5)

Tìm giao điểm của mặt phẳng \(\left( {BGK} \right)\) và \(AD\).

Bài 6b (1 điểm) Xét tính tăng, giảm của dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \dfrac{{3n - 1}}{{n + 1}}\).

Bài 7b (1,5 điểm) Câu lạc bộ văn nghệ của trường gồm 7 học sinh lớp 12, 15 học sinh lớp 11 và 13 học sinh lớp 10. Nhà trường chọn ngẫu nhiên 5 học sinh từ câu lạc bộ văn nghệ để tham gia một tiết mục văn nghệ trong lễ bế giảng. Tính xác suất sao cho trong 5 học sinh đó có đầy đủ cả ba khối lớp và có đúng 2 học sinh lớp 12.

III. Dành cho lớp 11TH1, 11TH2

Bài 5c (1,5 điểm) (Làm tiếp bài 5)

Gọi \(\left( P \right)\) là mặt phẳng chứa \(IO\) và song song với \(EH\). Xác định thiết diện của \(\left( P \right)\) với hình chóp \(S.ABCD\).

Bài 6c (1 điểm) Xét tính tăng, giảm của dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \dfrac{{n + 1}}{{n + 2}}\).

Bài 7c (1,5 điểm) Một hộp đựng 12 viên bi, trong đó có 7 viên vi màu đỏ, 5 viên bi màu xanh. Lấy ngẫu nhiên một lần 3 viên bi. Tính xác suất để lấy được 2 viên bi màu xanh trong 3 viên bi lấy ra.

IV. Dành cho lớp 11CT

Bài 5d (2 điểm) Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\), \(SA = a\sqrt 3 \). Gọi \(H,\,\,M\) lần lượt là trung điểm của \(AB\) và \(BC\). Biết rằng \(SH \bot \left( {ABCD} \right)\).

1) Tính góc giữa hai đường thẳng \(SC\) và \(AD\).

2) Chứng minh \(AM \bot HD\) và \(AM \bot SD\).

Bài 6d (1 điểm) Tính giới hạn sau: \(\lim \dfrac{{{1^2} + {2^2} + ... + {n^2}}}{{n\sqrt {{1^3} + {2^3} + ... + {n^3}} }}\).

Bài 7d (1 điểm) Cho dãy số \(\left( {{u_n}} \right)\) xác định bởi \(\left\{ \begin{array}{l}{u_1} = 1\\{u_{n + 1}} = \dfrac{{n + 1}}{{2n}}\,\,\left( {{u_n} + 2} \right)\,\,\forall n \in {\mathbb{N}^*}\end{array} \right.\).

Chứng minh rằng dãy số \(\left( {{u_n}} \right)\) có giới hạn hữu hạn và tính giới hạn đó.

 

HƯỚNG DẪN GIẢI CHI TIẾT

Thực hiện: Ban chuyên môn

A. PHẦN CHUNG:

Bài 1 (VD):

Phương pháp:

Giải phương trình bằng phương pháp đưa về phương trình tích sau đó giải các phương trình lượng giác cơ bản.

Cách giải:

\(\begin{array}{l}\,\,\,\,\,\,4\sin x\cos x + 2\sin x - 2\sqrt 3 \cos x - \sqrt 3  = 0\\ \Leftrightarrow 2\sin x\left( {2\cos x + 1} \right) - \sqrt 3 \left( {2\cos x + 1} \right) = 0\\ \Leftrightarrow \left( {2\cos x + 1} \right)\left( {2\sin x - \sqrt 3 } \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}2\cos x + 1 = 0\\2\sin x - \sqrt 3  = 0\end{array} \right. \\\Leftrightarrow \left[ \begin{array}{l}\cos x =  - \dfrac{1}{2}\\\sin x = \dfrac{{\sqrt 3 }}{2}\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{2\pi }}{3} + k2\pi \\x =  - \dfrac{{2\pi }}{3} + k2\pi \\x = \dfrac{\pi }{3} + m2\pi \\x = \dfrac{{2\pi }}{3} + m2\pi \end{array} \right. \\\Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{2\pi }}{3} + k2\pi \\x = \dfrac{\pi }{3} + m\pi \end{array} \right.\,\,\,\,\left( {k,\,\,m \in \mathbb{Z}} \right).\end{array}\)

Vậy phương trình có nghiệm: \(\left[ \begin{array}{l}x = \dfrac{{2\pi }}{3} + k2\pi \\x = \dfrac{\pi }{3} + m\pi \end{array} \right.\,\,\,\left( {k,\,\,m \in \mathbb{Z}} \right).\)

Bài 2 (TH):

Phương pháp:

Sử dụng công thức khai triển nhị thức Newton: \({\left( {a + b} \right)^n} = \sum\limits_{k = 0}^n {C_n^k{a^{n - k}}{b^k}.} \)

Cách giải:

Ta có: \({\left( {{x^3} - \dfrac{3}{x}} \right)^8} = \sum\limits_{k = 0}^8 {C_8^k{x^{3\left( {8 - k} \right)}}{{\left( { - \dfrac{3}{x}} \right)}^k}}  \\= \sum\limits_{k = 0}^8 {C_8^k{{\left( { - 3} \right)}^k}{x^{24 - 4k}}} .\)

Để có hệ số không chứa \(x\) trong khai triển thì: \(24 - 4k = 0 \Leftrightarrow k = 6\,\,\,\left( {tm} \right).\)

Vậy hệ số của số hạng không chứa \(x\) trong khai triển là: \(C_8^6{\left( { - 3} \right)^6} = 20412.\)

Bài 3 (VD):

Phương pháp:

Với mọi biến cố ta luôn có: \(P\left( {\overline A } \right) = 1 - P\left( A \right).\)

Cách giải:

Gọi biến cố \(A\): ‘‘Có ít nhất hai xạ thủ bắn trúng đích’’.

Khi đó ta có biến cố \(\overline A \): “Không có xạ thủ nào bắn trúng đích hoặc chỉ có một xạ thủ bắn trúng đích”.

Xác suất để xạ thủ thứ nhất không bắn trúng đích là: \(1 - 0,5 = 0,5.\)

Xác suất để xạ thủ thứ hai không bắn trúng đích là: \(1 - 0,6 = 0,4.\)

Xác suất để xạ thủ thứ ba không bắn trúng đích là: \(1 - 0,8 = 0,2.\)

Xác suất để cả 3 xạ thủ đều không bắn trúng đích là: \({P_1} = 0,5.0,4.0,2 = 0,04.\)

Xác suất để có 1 xạ thủ không bắn trúng địch là: \({P_2} = 0,5.0,6.0.8 + 0,5.0,4.0,8 + 0,5.0,6.0,2 = 0,46.\)

\( \Rightarrow P\left( {\overline A } \right) = 0,04 + 0,46 = 0,5.\)

Vậy \(P\left( A \right) = 1 - P\left( {\overline A } \right) = 1 - 0,5 = 0,5.\)

Bài 4 (VD):

Phương pháp:

Áp dụng công thức của cấp số cộng để làm bài toán.

Tổng của \(n\) số hạng đầu của CSC có số hạng đầu \({u_1}\) và công sai \(d\) là: \({S_n} = \dfrac{{\left[ {2{u_1} + \left( {n - 1} \right)d} \right]n}}{2}.\)

Cách giải:

Ngày 01/08/2018 bạn Bình bỏ vào ống heo \(500\)  đồng, ta coi \({u_1} = 500\) đồng.

Bắt đầu từ ngày thứ hai bạn Bình bỏ vào ống heo tăng thêm \(500\) đồng nữa nên \(d = 500.\)

Tháng 8/2019 có \(31\) ngày và tính đến hết ngày 29/09/2019 thì bạn Bình có thể tiết kiệm tiền được \(60\) ngày.

Số tiền bạn Bình bỏ ông heo sau \(60\) ngày là:

\({S_{61}} = \dfrac{{\left[ {2{u_1} + \left( {n - 1} \right)d} \right]n}}{2} \\= \dfrac{{\left( {2.500 + 59.500} \right).60}}{2} = 915\,000 đồng.\)

Như vậy sau thời gian bạn Bình tiết kiệm tiền, bạn Bình có đủ tiền để mua quà sinh nhật cho mẹ vào ngày 30/09/2019.

Bài 5 (VD):

Phương pháp:

a) Chứng minh \(IO//SE \Rightarrow IO//\left( {SAD} \right).\)

b) Chứng minh \(\left\{ \begin{array}{l}GK//EG\\EM//IG\end{array} \right. \Rightarrow \left( {GHI} \right)//\left( {AHM} \right).\)

Cách giải:

Cho hình chóp \(SABCD\) có đáy là hình bình hành tâm \(O.\) Gọi \(E,\,\,H,\,\,F\) lần lượt là trung điểm của \(AD,\,\,DC,\,\,CB.\)

 

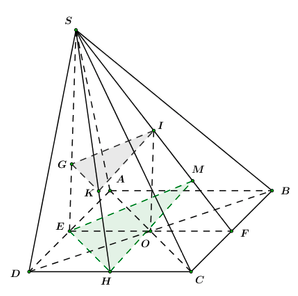
1) Gọi \(I\) là trung điểm của \(SF.\) Chứng minh \(IO\) song song với mặt phẳng \(\left( {SAD} \right).\)

Xét \(\Delta SEF\) ta có:

\(I,\,\,O\) lần lượt là trung điểm của \(SF,\,\,EF\)

\( \Rightarrow OI\) là đường trung bình của \(\Delta SEF.\)  (định nghĩa)

\( \Rightarrow OI//SE\) (tính chất)

Mà \(SE \subset \left( {SAD} \right) \Rightarrow OI//\left( {SAD} \right)\,\,\,\,\left( {dpcm} \right).\)

2) Gọi \(G,\,\,K\) lần lượt là trọng tâm của \(\Delta SAD,\,\,\Delta SCD,\,\,M\) là trung điểm của \(IF.\) Chứng minh rằng mặt phẳng \(\left( {GKI} \right)\) song song với mặt phẳng \(\left( {EHM} \right).\) 

Ta có: \(G,\,\,K\) lần lượt là trọng tâm \(\Delta SAD\) và \(\Delta SCD\) (gt)

\( \Rightarrow \dfrac{{SG}}{{SE}} = \dfrac{{SK}}{{SH}} = \dfrac{2}{3} \Rightarrow GK//EH\) (định lý Talet đảo).

Ta có: \(I,\,\,M\) là trung điểm của \(SF,\,\,IF \Rightarrow \dfrac{{SI}}{{SM}} = \dfrac{2}{3}.\)

Xét \(\Delta SEM\) ta có: \(\dfrac{{SG}}{{SE}} = \dfrac{{AI}}{{SM}} = \dfrac{2}{3}\,\,\,\left( {cmt} \right)\)

\( \Rightarrow GI//EM\) (định lý Talet đảo).

Mà \(\left\{ \begin{array}{l}GK,\,\,GI \subset \left( {IGK} \right)\\EH,\,\,EM \subset \left( {EMH} \right)\end{array} \right. \\\Rightarrow \left( {IGK} \right)//\left( {EMH} \right)\,\,\,\,\left( {dpcm} \right).\)

B. PHẦN RIÊNG:

I. Dành cho lớp 11A1, 11A2, 11CL, 11CH, HCS.

Bài 5a (VD):

Phương pháp:

Xác định mặt phẳng \(\left( P \right)\) sau đó tìm thiết diện của hình chóp. Mặt phẳng \(\left( P \right)\) chính là mặt phẳng \(\left( {MEH} \right).\)

Cách giải:

Gọi \(\left( P \right)\) là mặt phẳng chứa \(EH\) và song song với \(IG.\) Xác định thiết diện của mặt phẳng \(\left( P \right)\) với hình chóp \(SABCD.\)

 

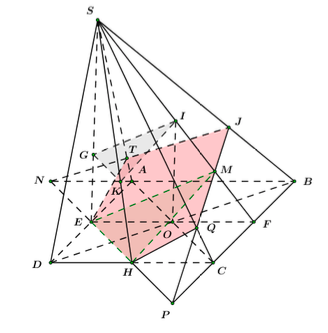
Ta có: \(GI//EM\,\,\,\left( {cmt} \right) \Rightarrow GI//\left( {EMH} \right).\)

Lại có: \(\left( P \right) \supset EH,\,\,\,\left( P \right)//GI \Rightarrow \left( P \right) \equiv \left( {EMH} \right).\)

Trong mặt phẳng \(\left( {ABCD} \right)\) kéo dài \(EH\) cắt \(BC\) tại \(P,\) cắt \(AB\) tại \(N.\)

Trong mặt phẳng \(\left( {SBC} \right),\) kéo dài \(PM\) cắt \(SC\) tại \(Q\) và cắt \(SB\)tại \(J.\)

Trong mặt phẳng \(\left( {SAB} \right),\) nối \(J\) và \(N\) cắt \(SA\) tại \(T.\)

 Khi đó ta có:

\(\begin{array}{l}\left( {EMH} \right) \cap \left( {SAB} \right) = JT\\\left( {EMH} \right) \cap \left( {SAD} \right) = TE\\\left( {EMH} \right) \cap \left( {ABCD} \right) = EH\\\left( {EMH} \right) \cap \left( {SDC} \right) = HQ\\\left( {EMH} \right) \cap \left( {SBC} \right) = QJ\end{array}\)

Vậy thiết diện cần tìm là ngũ giác \(JTEHQ.\)

Bài 6a (VD):

Xét tính tăng, giảm cũa dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \dfrac{n}{{{n^2} + 1}}.\)

Phương pháp:

Xét hiệu: \(A = {u_{n + 1}} - {u_n}.\)

+) Nếu \(A > 0\) thì \({u_n}\) là dãy số tăng.

+) Nếu \(A < 0\) thì \({u_n}\) là dãy số giảm.

Cách giải:

Ta có: \({u_{n + 1}} = \dfrac{{n + 1}}{{{{\left( {n + 1} \right)}^2} + 1}} = \dfrac{{n + 1}}{{{n^2} + 2n + 2}}.\)

Xét hiệu: \(A = {u_{n + 1}} - {u_n} = \dfrac{{n + 1}}{{{n^2} + 2n + 2}} - \dfrac{n}{{{n^2} + 1}}\)

\(\begin{array}{l} \Rightarrow A = \dfrac{{\left( {n + 1} \right)\left( {{n^2} + 1} \right) - n\left( {{n^2} + 2n + 2} \right)}}{{\left( {{n^2} + 1} \right)\left( {{n^2} + 2n + 2} \right)}}\\\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{{n^3} + n + {n^2} + 1 - {n^3} - 2{n^2} - 2n}}{{\left( {{n^2} + 1} \right)\left( {{n^2} + 2n + 2} \right)}}\\\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{ - {n^2} - n + 1}}{{\left( {{n^2} + 1} \right)\left( {{n^2} + 2n + 2} \right)}}.\end{array}\)

Với \(\forall n\, \in {\mathbb{N}^*}\) ta có: \(\left\{ \begin{array}{l} - {n^2} - n + 1 < 0\\\left( {{n^2} + 1} \right)\left( {{n^2} + 2n + 2} \right) > 0\end{array} \right. \Rightarrow A < 0\) hay \({u_{n + 1}} < {u_n}\,\,\forall n \in {\mathbb{N}^*}\).

\( \Rightarrow \) Dãy số \(\left( {{u_n}} \right) = \dfrac{n}{{{n^2} + 1}}\) là dãy số giảm.

Bài 7a (VD):

Phương pháp:

Xác suất của biến cố \(A\)  là: \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega  \right)}}.\)

Cách giải:

Xếp 4 đội của nhóm 1 vào 4 bảng có 4! cách xếp.

Xếp 4 đội của nhóm 2 vào 4 bảng có 4! cách xếp.

Xếp 4 đội của nhóm 3 vào 4 bảng có 4! cách xếp.

Xếp 4 đội của nhóm 4 vào 4 bảng có 4! cách xếp.

\( \Rightarrow n\left( \Omega  \right) = {\left( {4!} \right)^4}\).

Gọi biến cố \(A:\) ‘‘Không có bảng nào có nhiều hơn một đội của khu vực Đông Nam Á’’.  Như vậy mỗi bảng đấu phải có một đội của khu vực Đông Nam Á.

Xếp 4 đội Đông Nam Á vào 4 bảng có 4! cách xếp.

Mỗi bảng chứa 1 đội Đông Nam Á của nhóm bất kì, nên phải xếp 3 đội còn lại của nhóm chứa đội Đông Nam Á đó vào 3 bảng còn lại, có \(3!\) cách xếp.

Tương tự cho 3 bảng còn lại.

\( \Rightarrow n\left( A \right) = 4!{\left( {3!} \right)^4}\).

Vậy \(P\left( A \right) = \dfrac{{4!{{\left( {3!} \right)}^4}}}{{{{\left( {4!} \right)}^4}}} = \dfrac{3}{{32}}\).

II. Dành cho lớp 11CA1, 11CA2, 11CA3, 11CV

Bài 5b (VD)

Phương pháp:

- Chọn \(AD \subset \left( \alpha  \right)\) nào đó.

- Tìm \(d = \left( {BKG} \right) \cap \left( \alpha  \right)\).

- Xác định \(P = AD \cap d,\) chứng minh \(P = AD \cap \left( {BGK} \right)\).

Cách giải:

(Làm tiếp bài 5)

Tìm giao điểm của mặt phẳng \(\left( {BGK} \right)\) và \(AD\).

 

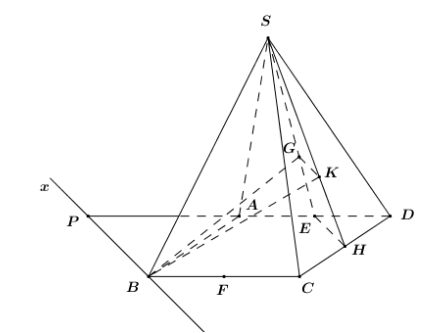
Vì \(G\) là trọng tâm tam giác \(SAD\) nên \(\dfrac{{SG}}{{SE}} = \dfrac{2}{3}\) (Tính chất trọng tâm).

Vì \(K\) là trọng tâm tam giác \(SCD\) nên \(\dfrac{{SK}}{{SH}} = \dfrac{2}{3}\) (Tính chất trọng tâm).

\( \Rightarrow \dfrac{{SG}}{{SE}} = \dfrac{{SK}}{{SH}} = \dfrac{2}{3} \Rightarrow GK\parallel EH\) (Định lí Ta-lét đảo).

Chọn \(AD \subset \left( {ABCD} \right)\), tìm giao tuyến của \(\left( {BGK} \right)\) và \(\left( {ABCD} \right)\).

+ \(B\) là điểm chung thứ nhất.

+ \(\left\{ \begin{array}{l}\left( {BGK} \right) \supset GK\\\left( {ABCD} \right) \supset EH\\GK\parallel EH\,\,\left( {cmt} \right)\end{array} \right. \Rightarrow \) Giao tuyến của \(\left( {BGK} \right)\) và \(\left( {ABCD} \right)\) là đường thẳng đi qua \(B\) và song song với \(GK,\,\,EH\).

Trong \(\left( {ABCD} \right)\) qua \(B\) kẻ \(Bx\parallel GK\parallel EH \Rightarrow \left( {BGK} \right) \cap \left( {ABCD} \right) = Bx\).

Trong \(\left( {ABCD} \right)\) gọi \(P = Bx \cap AD\) ta có:

\(\left\{ \begin{array}{l}P \in AD\\P \in Bx \subset \left( {BGK} \right) \Rightarrow P \in \left( {BGK} \right)\end{array} \right. \Rightarrow P = AD \cap \left( {BGK} \right)\).

Bài 6b (VD)

Phương pháp:

Xét hiệu \(H = {u_{n + 1}} - {u_n}\) và kết luận về tính tăng giảm của dãy số.

Cách giải:

Xét hiệu: \(H = {u_{n + 1}} - {u_n}\)

\(\begin{array}{l}H = \dfrac{{3n + 2}}{{n + 2}} - \dfrac{{3n - 1}}{{n + 1}}\\H = \dfrac{{\left( {3n + 2} \right)\left( {n + 1} \right) - \left( {3n - 1} \right)\left( {n + 2} \right)}}{{\left( {n + 2} \right)\left( {n + 1} \right)}}\\H = \dfrac{{3{n^2} + 5n + 2 - 3{n^2} - 5n + 2}}{{\left( {n + 2} \right)\left( {n + 1} \right)}}\\H = \dfrac{4}{{\left( {n + 2} \right)\left( {n + 1} \right)}}\end{array}\)

Ta thấy \(H > 0\,\,\forall n \in {\mathbb{N}^*} \Rightarrow {u_{n + 1}} > {u_n}\,\,\forall n \in {\mathbb{N}^*}\).

Vậy dãy \(\left( {{u_n}} \right)\) đã cho là dãy tăng.

Bài 7b (VD)

Phương pháp:

- Chọn 2 học sinh khối 12.

- Chọn 3 học sinh còn lại có 2 TH:

   TH1: 2 học sinh khối 11 và 1 học sinh khối 10.

   TH2: 1 học sinh khối 11 và 2 học sinh khối 10.

Cách giải:

Câu lạc bộ có tổng số học sinh là \(7 + 15 + 13 = 35\) (học sinh)

Chọn ngẫu nhiên 5 học sinh \( \Rightarrow n\left( \Omega  \right) = C_{35}^5\).

Gọi A là biến cố: “5 học sinh đó có đầy đủ cả ba khối lớp và có đúng 2 học sinh lớp 12”.

Số cách chọn 2 học sinh lớp 12 là \(C_7^2\) cách.

Chọn 3 học sinh còn lại:

TH1: 2 học sinh khối 11 và 1 học sinh khối 10: có \(C_{15}^2.C_{13}^1\) cách.

TH2: 1 học sinh khối 11 và 2 học sinh khối 10: có \(C_{15}^1.C_{13}^2\) cách.

\( \Rightarrow \) số cách chọn 3 học sinh còn lại là: \(C_{15}^2.C_{13}^1 + C_{15}^1.C_{13}^2\) cách.

Áp dụng quy tắc nhân ta có: \(n\left( A \right) = C_7^2\left( {C_{15}^2.C_{13}^1 + C_{15}^1.C_{13}^2} \right)\).

Vậy xác suất của biến cố A là \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega  \right)}} = \dfrac{{C_7^2\left( {C_{15}^2.C_{13}^1 + C_{15}^1.C_{13}^2} \right)}}{{C_{35}^5}} = \dfrac{{7605}}{{46376}}\). 

III. Dành cho lớp 11TH1, 11TH2

Bài 5c (VD)

Phương pháp:

Xác định giao tuyến của \(\left( P \right)\) với các mặt của hình chóp.

Cách giải:

(Làm tiếp bài 5) Gọi \(\left( P \right)\) là mặt phẳng chứa \(IO\) và song song với \(EH\). Xác định thiết diện của \(\left( P \right)\) với hình chóp \(S.ABCD\).

 

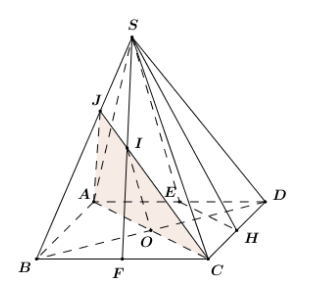
Vì \(E\) là trung điểm của \(AD\), \(H\) là trung điểm của \(CD\,\,\left( {gt} \right)\).

\( \Rightarrow EH\) là đường trung bình của tam giác \(ADC\).

\( \Rightarrow EH\parallel AC\) (Tính chất đường trung bình).

Xét \(\left( P \right)\) và \(\left( {ABCD} \right)\) có:

+ \(O\) là điểm chung thứ nhất.

+ \(\left\{ \begin{array}{l}\left( P \right)\parallel EH\\EH \subset \left( {ABCD} \right)\end{array} \right. \Rightarrow \) Giao tuyến của \(\left( P \right)\) và \(\left( {ABCD} \right)\) là đường thẳng qua \(O\) và song song với \(EH\).

\( \Rightarrow \left( P \right) \cap \left( {ABCD} \right) = AC\).

\( \Rightarrow AC \subset \left( P \right)\).

Trong \(\left( {SBC} \right)\) kéo dài \(IC\) cắt \(SB\) tại \(J\), khi đó ta có:

\(\begin{array}{l}\left( P \right) \cap \left( {SAB} \right) = AJ\\\left( P \right) \cap \left( {SBC} \right) = JC\\\left( P \right) \cap \left( {ABCD} \right) = AC\end{array}\)

Vậy thiết diện của hình chóp cắt bởi \(\left( P \right)\) là tam giác \(ACJ\).

Bài 6c (VD)

Phương pháp:

Xét hiệu \(H = {u_{n + 1}} - {u_n}\) và kết luận về tính tăng giảm của dãy số.

Cách giải:

Xét hiệu: \(H = {u_{n + 1}} - {u_n}\)

\(\begin{array}{l}H = \dfrac{{n + 2}}{{n + 3}} - \dfrac{{n + 1}}{{n + 2}}\\H = \dfrac{{{{\left( {n + 2} \right)}^2} - \left( {n + 1} \right)\left( {n + 3} \right)}}{{\left( {n + 3} \right)\left( {n + 2} \right)}}\\H = \dfrac{{{n^2} + 4n + 4 - {n^2} - 4n + 3}}{{\left( {n + 3} \right)\left( {n + 2} \right)}}\\H = \dfrac{1}{{\left( {n + 3} \right)\left( {n + 2} \right)}}\end{array}\)

Ta thấy \(H > 0\,\,\forall n \in {\mathbb{N}^*} \Rightarrow {u_{n + 1}} > {u_n}\,\,\forall n \in {\mathbb{N}^*}\).

Vậy dãy \(\left( {{u_n}} \right)\) đã cho là dãy tăng.

Bài 7c (VD)

Phương pháp:

- Tính không gian mẫu.

- Tính số kết quả thuận lợi cho biến cố: Lấy 2 viên bi xanh + 1 viên bi đỏ.

- Tính xác suất của biến cố.

Cách giải:

Lấy ra một lần 3 viên bi \( \Rightarrow n\left( \Omega  \right) = C_{12}^3\).

Gọi A là biến cố: “Lấy được 2 viên bi màu xanh trong 3 viên bi lấy ra”

Lấy 2 viên bi màu xanh có \(C_5^2\) cách.

Lấy 1 viên bi màu đỏ có \(C_7^1\) cách.

Áp dụng quy tắc nhân ta có \(n\left( A \right) = C_5^2.C_7^1\).

Vậy xác suất của biến cố A là: \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega  \right)}} = \dfrac{{C_5^2.C_7^1}}{{C_{12}^3}} = \dfrac{7}{{22}}\).

IV. Dành cho lớp 11CT

Bài 5d (VD)

Phương pháp:

1) Chứng minh \(\angle \left( {SC;AD} \right) = \angle \left( {SC;BC} \right)\).

    Chứng minh \(\Delta SBC\) vuông và tính các giá trị lượng giác của góc cần tìm.

2) Chứng minh \(\overrightarrow {AM} .\overrightarrow {HD}  = 0\).

    Chứng minh \(AM\) vuông góc với mặt phẳng chứa \(SD\).

Cách giải:

Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\), \(SA = a\sqrt 3 \). Gọi \(H,\,\,M\) lần lượt là trung điểm của \(AB\) và \(BC\). Biết rằng \(SH \bot \left( {ABCD} \right)\).

 

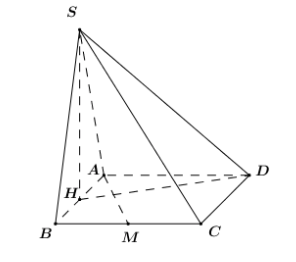
1) Tính góc giữa hai đường thẳng \(SC\) và \(AD\).

Vì \(AD\parallel BC\,\,\left( {gt} \right) \Rightarrow \angle \left( {SC;AD} \right) = \angle \left( {SC;BC} \right)\).

Ta có: \(BC \bot AD\) (\(ABCD\) là hình vuông)

          \(SH \bot \left( {ABCD} \right) \Rightarrow SH \bot BC\).

Mà \(AB,\,\,SH\) cắt nhau, nằm trong mặt phẳng \(\left( {SAB} \right)\).

\( \Rightarrow BC \bot \left( {SAB} \right)\). Mà \(SB \subset \left( {SAB} \right) \Rightarrow BC \bot SB\).

\( \Rightarrow \Delta SBC\) vuông tại \(B \Rightarrow \angle \left( {SC;BC} \right) = \angle SCB\) (do \(\angle SCB < {90^0}\)).

Xét tam giác \(SAB\) có: \(SH \bot \left( {ABCD} \right) \Rightarrow SH \bot AB \Rightarrow SH\) là đường cao đồng thời là trung tuyến.

\( \Rightarrow \Delta SAB\) cân tại \(S \Rightarrow SA = SB = a\sqrt 3 \).

Trong tam giác vuông \(SBC\) ta có: \(\tan \angle SCB = \dfrac{{SB}}{{BC}} = \dfrac{{a\sqrt 3 }}{a} = \sqrt 3 \).

Vậy \(\angle SCB = {60^0}\) hay \(\angle \left( {SC;AD} \right) = {60^0}\).

2) Chứng minh \(AM \bot HD\) và \(AM \bot SD\)

Ta xét tích vô hướng sau:

\(\begin{array}{l}\overrightarrow {AM} .\overrightarrow {HD}  = \left( {\overrightarrow {AB}  + \overrightarrow {BM} } \right)\left( {\overrightarrow {HA}  + \overrightarrow {AD} } \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left( {\overrightarrow {AB}  + \dfrac{1}{2}\overrightarrow {BC} } \right)\left( { - \dfrac{1}{2}\overrightarrow {AB}  + \overrightarrow {AD} } \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \overrightarrow {AB} .\left( { - \dfrac{1}{2}\overrightarrow {AB} } \right) + \overrightarrow {AB} .\overrightarrow {AD}  + \dfrac{1}{2}\overrightarrow {BC} .\left( { - \dfrac{1}{2}\overrightarrow {AB} } \right) + \dfrac{1}{2}\overrightarrow {BC} .\overrightarrow {AD} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, =  - \dfrac{1}{2}A{B^2} + 0 + 0 + \dfrac{1}{2}B{C^2}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, =  - \dfrac{1}{2}{a^2} + \dfrac{1}{2}{a^2} = 0\end{array}\)

Do đó \(AM \bot HD\).

Vì \(SH \bot \left( {ABCD} \right) \supset AM \Rightarrow SH \bot AM\).

Ta có: \(\left\{ \begin{array}{l}AM \bot HD\,\,\left( {cmt} \right)\\AM \bot SD\,\,\,\left( {cmt} \right)\\HD \cap SD \subset \left( {SHD} \right)\end{array} \right. \Rightarrow AM \bot \left( {SHD} \right)\).

Mà \(SD \subset \left( {SHD} \right)\). Vậy \(AM \bot SD\) (đpcm).

Bài 6d (VDC)

Phương pháp:

- Sử dụng phương pháp quy nạp toán học, chứng minh \({1^3} + {2^3} + ... + {n^3} = {\left[ {\dfrac{{n\left( {n + 1} \right)}}{2}} \right]^2}\,\,\forall n \in {\mathbb{N}^*}\) và \({1^2} + {2^2} + ... + {n^2} = \dfrac{{n\left( {n + 1} \right)\left( {2n + 1} \right)}}{6}\,\,\forall n \in {\mathbb{N}^*}\).

- Thay các biểu thức đã được chứng minh vào biểu thức ban đầu và tính giới hạn.

Cách giải:

Trước hết, ta chứng minh \({1^3} + {2^3} + ... + {n^3} = {\left[ {\dfrac{{n\left( {n + 1} \right)}}{2}} \right]^2}\,\,\forall n \in {\mathbb{N}^*}\) (1) theo phương pháp quy nạp toán học.

Với \(n = 1\) ta có: \(VT = {1^3} = 1,\,\,VP = \left( {{{\dfrac{{1.2}}{2}}^2}} \right) = 1 \Rightarrow VT = VP\).

Do đó (1) đúng với \(n = 1\).

Giả sử (1) đúng với \(n = k \ge 1\), tức là \({1^3} + {2^3} + ... + {k^3} = {\left[ {\dfrac{{k\left( {k + 1} \right)}}{2}} \right]^2}\). Ta cần chứng minh (1) đúng với \(n = k + 1\), tức là cần chứng minh \({1^3} + {2^3} + ... + {k^3} + {\left( {k + 1} \right)^3} = {\left[ {\dfrac{{\left( {k + 1} \right)\left( {k + 2} \right)}}{2}} \right]^2}\).

Theo giả thiết quy nạp, ta có:

\(\begin{array}{l}VT = {\left[ {\dfrac{{k\left( {k + 1} \right)}}{2}} \right]^2} + {\left( {k + 1} \right)^3}\\\,\,\,\,\,\,\, = \dfrac{{{k^2}{{\left( {k + 1} \right)}^2}}}{4} + {\left( {k + 1} \right)^3}\\\,\,\,\,\,\, = \dfrac{{{{\left( {k + 1} \right)}^2}\left( {{k^2} + 4k + 4} \right)}}{4}\\\,\,\,\,\,\, = \dfrac{{{{\left( {k + 1} \right)}^2}{{\left( {k + 2} \right)}^2}}}{4}\\\,\,\,\,\,\, = {\left[ {\dfrac{{\left( {k + 1} \right)\left( {k + 2} \right)}}{2}} \right]^2} = VP\end{array}\)

Do đó (1) đúng với mọi \(n \in {\mathbb{N}^*}\).

Tương tự bằng quy nạp toán học ta chứng minh được \({1^2} + {2^2} + ... + {n^2} = \dfrac{{n\left( {n + 1} \right)\left( {2n + 1} \right)}}{6}\,\,\forall n \in {\mathbb{N}^*}\) (2) như sau:

Với \(n = 1\) ta có \(VT = {1^2} = 1,\,\,VP = \dfrac{{1.2.3}}{6} = 1 \Rightarrow VT = VP\).

Do đó (2) đúng với \(n = 1\).

Giả sử (2) đúng với \(n = k \ge 1\), tức là \({1^2} + {2^2} + ... + {k^2} = \dfrac{{k\left( {k + 1} \right)\left( {2k + 1} \right)}}{6}\), ta cần chứng minh (2) đúng với \(n = k + 1\), tức là cần chứng minh \({1^2} + {2^2} + ... + {k^2} + {\left( {k + 1} \right)^2} = \dfrac{{\left( {k + 1} \right)\left( {k + 2} \right)\left( {2k + 3} \right)}}{6}\).

Theo giả thiết quy nạp, ta có:

\(\begin{array}{l}VT = \dfrac{{k\left( {k + 1} \right)\left( {2k + 1} \right)}}{6} + {\left( {k + 1} \right)^2}\\\,\,\,\,\,\,\, = \left( {k + 1} \right)\dfrac{{2{k^2} + k + 6k + 6}}{6}\\\,\,\,\,\,\,\, = \left( {k + 1} \right)\dfrac{{2{k^2} + 7k + 6}}{6}\\\,\,\,\,\,\,\, = \dfrac{{\left( {k + 1} \right)\left( {k + 2} \right)\left( {2k + 3} \right)}}{6} = VP\end{array}\)

Như vậy, (2) đúng với mọi \(n \in {\mathbb{N}^*}\).

Khi đó ta có: 

\(\begin{array}{l}\dfrac{{{1^2} + {2^2} + ... + {n^2}}}{{n\sqrt {{1^3} + {2^3} + ... + {n^3}} }} = \dfrac{{\dfrac{{n\left( {n + 1} \right)\left( {2n + 1} \right)}}{6}}}{{n\sqrt {{{\left[ {\dfrac{{n\left( {n + 1} \right)}}{2}} \right]}^2}} }}\\ = \dfrac{{\dfrac{{n\left( {n + 1} \right)\left( {2n + 1} \right)}}{6}}}{{n.\dfrac{{n\left( {n + 1} \right)}}{2}}} = \dfrac{{2n + 1}}{{3n}}\end{array}\)

Vậy \(\lim \dfrac{{{1^2} + {2^2} + ... + {n^2}}}{{n\sqrt {{1^3} + {2^3} + ... + {n^3}} }} = \lim \dfrac{{2n + 1}}{{3n}} = \dfrac{2}{3}\).

Bài 7d (VDC)

Cách giải:

Giả sử dãy số \(\left( {{u_n}} \right)\) tồn tại giới hạn hữu hạn và \(\lim {u_n} = a\,\,\left( {a \in \mathbb{R}} \right)\).

Ta có: \(\lim \dfrac{{n + 1}}{{2n}} = \lim \dfrac{{1 + \dfrac{1}{n}}}{2} = \dfrac{1}{2}\).

Từ giả thiết \({u_{n + 1}} = \dfrac{{n + 1}}{{2n}}\,\,\left( {{u_n} + 2} \right)\) ta có:

\(\begin{array}{l}\lim {u_{n + 1}} = \lim \left[ {\dfrac{{n + 1}}{{2n}}\,\,\left( {{u_n} + 2} \right)} \right]\\ \Rightarrow a = \dfrac{1}{2}\left( {a + 2} \right) \Leftrightarrow a = \dfrac{1}{2}a + 1 \Leftrightarrow a = 2\end{array}\).

Vậy dãy số \(\left( {{u_n}} \right)\) tồn tại giới hạn và \(\lim {u_n} = 2\).