Đề thi học kì 1 môn toán lớp 11 năm 2019 - 2020 sở GDĐT Bắc Ninh

Câu 1  (3,0 điểm).

1) Tìm tập xác định hàm số \(f\left( x \right) = \dfrac{1}{{\cos x - 1}} \cdot \)

2) Giải phương trình \(2{\sin ^2}x - 5\sin x + 2 = 0.\)

3) Tìm tất cả các giá trị nguyên của tham số \(m\) để phương trình sau có nghiệm \(3\sin x + m\cos x = 2m.\)

Câu 2 (2,5 điểm).

Từ một tập gồm \(10\) câu hỏi trong đó có \(4\) câu lí thuyết và \(6\) câu bài tập, người ta tạo thành các đề thi. Biết rằng một đề thi phải gồm \(3\) câu hỏi trong \(10\) câu hỏi trên.

a, Hỏi có bao nhiêu cách tạo ra các đề thi.

b, Tính xác suất để trong một đề thi phải có ít nhất một câu lý thuyết và một câu bài tập.

Câu 3 (1,0 điểm).

Trong mặt phẳng tọa độ \(Oxy,\) cho đường thẳng \(d:2x - y - 1 = 0.\) Viết phương trình đường thẳng \(d'\) là ảnh của đường thẳng \(d\) qua phép tịnh tiến theo véc tơ \(\overrightarrow u  = \left( {3; - 1} \right).\)

Câu 4 (3,0 điểm).

Cho hình chóp \(S.ABC.\) Gọi \(K,N\) lần lượt là trung điểm của \(SA,BC.\) Điểm \(M\) thuộc cạnh \(SC\) sao cho \(SM = \dfrac{2}{3}SC.\)

a, Tìm giao tuyến của hai mặt phẳng \(\left( {KMN} \right)\) và \(\left( {SBC} \right).\)

b, Tìm giao điểm của đường thẳng \(AC\) và mặt phẳng \(\left( {KMN} \right).\)

c, Gọi \(H\) là giao điểm của đường thẳng \(AB\) và mặt phẳng \(\left( {KMN} \right).\) Chứng minh rằng ba đường thẳng \(KH,MN,SB\) đồng quy.

Câu 5 (0,5 điểm).

Cho số nguyên dương \(n\) thỏa mãn \(C_n^3C_n^{n - 3} - 2C_n^3C_{n - 1}^2 + C_{n - 1}^2C_{n - 1}^{n - 3} = 14400.\) Tìm hệ số của số hạng chứa \({x^9}\) trong khai triển \(T\left( x \right) = {\left( {8{x^6} - 36{x^3} - \dfrac{{27}}{{{x^3}}} + 54} \right)^n},\) với \(x \ne 0.\)

HẾT

HƯỚNG DẪN GIẢI CHI TIẾT

Thực hiện: Ban chuyên môn

Câu 1 (VD).

Phương pháp:

1) Biểu thức \(\dfrac{1}{{f\left( x \right)}}\) xác định nếu \(f\left( x \right) \ne 0\).

2) Giải phương trình bậc hai đối với ẩn là hàm \(\sin x\).

3) Phương trình \(a\sin x + b\cos x + c = 0\) có nghiệm \( \Leftrightarrow {a^2} + {b^2} \ge {c^2}\)

Cách giải:

1) Tìm tập xác định hàm số \(f\left( x \right) = \dfrac{1}{{\cos x - 1}} \cdot \)

Điều kiện xác định : \(\cos x \ne 1 \Leftrightarrow x \ne k2\pi ,\,k \in \mathbb{Z}.\)

Vậy tập xác định hàm số : \(D = \mathbb{R}\backslash \left\{ {k2\pi ,\,k \in \mathbb{Z}} \right\}.\)

2) Giải phương trình \(2{\sin ^2}x - 5\sin x + 2 = 0.\)

\(2{\sin ^2}x - 5\sin x + 2 = 0\) \( \Leftrightarrow \left[ \begin{array}{l}\sin x = 2\left( {VN} \right)\\\sin x = \dfrac{1}{2}\end{array} \right.\)

Với \(\sin x = \dfrac{1}{2} \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{6} + k2\pi \\x = \dfrac{{5\pi }}{6} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)

Vậy phương trình có các nghiệm là \(x = \dfrac{\pi }{6} + k2\pi ,\,\,x = \dfrac{{5\pi }}{6} + k2\pi \left( {k \in \mathbb{Z}} \right)\)

3) Tìm tất cả các giá trị nguyên của tham số \(m\) để phương trình sau có nghiệm \(3\sin x + m\cos x = 2m.\)

Phương trình có nghiệm \( \Leftrightarrow {3^2} + {m^2} \ge {\left( {2m} \right)^2} \Leftrightarrow {m^2} \le 3\) \( \Leftrightarrow  - \sqrt 3  \le m \le \sqrt 3 \)

Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 1;0;1} \right\}\)

Vậy có ba giá trị nguyên của \(m\) thỏa mãn là : \(m =  - 1;\,m = 0,\,m = 1.\)

Câu 2 (VD).

Phương pháp:

a) Mỗi cách lấy ra \(3\) trong \(10\) câu hỏi là một tổ hợp chập \(3\) của \(10\) phần tử.

b) Tính số phần tử của KGM \(n\left( \Omega  \right)\)

Tính số khả năng có lợi cho biến cố \(n\left( A \right)\)

Tính xác suất \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega  \right)}}\)

Cách giải:

a, Hỏi có bao nhiêu cách tạo ra các đề thi.

Mỗi một cách lấy ra \(3\) câu trong \(10\) câu để tạo thành một đề thi là một tổ hợp chập \(3\) của \(10.\)

Do đó số cách lấy ra là : \(C_{10}^3 = 120\) cách.

b, Tính xác suất để trong một đề thi phải có ít nhất một câu lý thuyết và một câu bài tập.

\(n\left( \Omega  \right) = C_{10}^3 = 120\)

Kí hiệu \(A:\) “tTrong một đề thi gồm \(3\) câu phải có ít nhất một câu lý thuyết và một câu bài tập”, ta chia các trường hợp :

TH1 : Đề thi gồm \(1\) câu lý thuyết và \(2\) câu bài tập có số cách chọn là \(C_4^1.C_6^2\) (cách)

TH2 : Đề thi gồm \(2\) câu lý thuyết và \(1\) câu bài tập có số cách chọn là \(C_4^2.C_6^1\) (cách)

Do đó \(n\left( A \right) = C_4^1.C_6^2 + C_4^2.C_6^1 = 96\)

Vậy xác suất cần tính là \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega  \right)}} = \dfrac{{96}}{{120}} = \dfrac{4}{5}.\)

Câu 3 (VD).

Phương pháp:

Gọi phương trình đường thẳng \(d'\) (chú ý \(d'//d\) hoặc \(d' \equiv d\))

Lấy một điểm \(A \in d\) và tìm ảnh \(A' = {T_{\overrightarrow v }}\left( A \right)\).

Thay tọa độ \(A'\) vào phương trình \(d'\) vừa gọi suy ra đáp số.

Cách giải:

Ta có \({T_{\overrightarrow u }}\left( d \right) = d' \Rightarrow \left[ \begin{array}{l}d//d'\\d \equiv d'\end{array} \right.\)

Phương trình đường thẳng \(d':2x - y + m = 0\)

Lấy điểm \(A\left( {0; - 1} \right) \in d\) và gọi \(A'\left( {x';y'} \right) = {T_{\overrightarrow u }}\left( A \right)\)

\( \Leftrightarrow \left\{ \begin{array}{l}x' = 3 + 0 = 3\\y' =  - 1 - 1 =  - 2\end{array} \right. \Rightarrow A'\left( {3; - 2} \right)\)

Điểm \(A'\left( {3; - 2} \right) \in d' \Leftrightarrow 2.3.\left( { - 2} \right) + m = 0 \Leftrightarrow m =  - 8.\)

Vậy phương trình đường thẳng \(d':2x - y - 8 = 0\).

Câu 4 (VD).

Phương pháp:

a) Tìm hai điểm chung của hai mặt phẳng suy ra giao tuyến.

b) Tìm một đường thẳng thuộc \(mp\left( {KMN} \right)\) mà cắt được đường thẳng \(AC\).

c) Tìm giao điểm \(H\), sử dụng định lí ba giao tuyến suy ra đồng quy.

Cách giải:

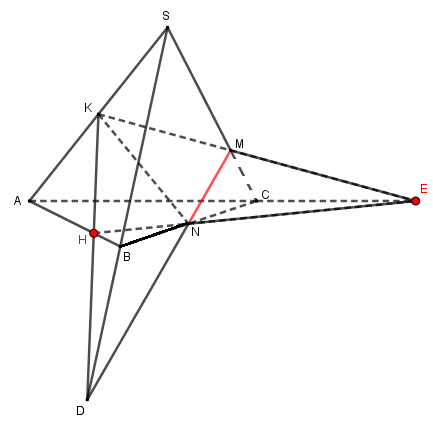
a, Tìm giao tuyến của hai mặt phẳng \(\left( {KMN} \right)\) và \(\left( {SBC} \right).\)

Ta có : \(M \in \left( {KMN} \right) \cap \left( {SBC} \right),\) \(N \in \left( {KMN} \right) \cap \left( {SBC} \right)\)

Do đó, \(\left( {KMN} \right) \cap \left( {SBC} \right) = MN\)

b, Tìm giao điểm của đường thẳng \(AC\) và mặt phẳng \(\left( {KMN} \right).\)

Trong mặt phẳng \(\left( {SAC} \right),\) vì \(\dfrac{{SK}}{{SA}} \ne \dfrac{{SM}}{{SC}}\) nên \(KM\) cắt \(AC\) tại \(E.\)

\( \Rightarrow \left\{ \begin{array}{l}E \in KM \subset \left( {KMN} \right)\\E \in AC\end{array} \right. \Rightarrow AC \cap \left( {KMN} \right) = E\)

c, Gọi \(H\) là giao điểm của đường thẳng \(AB\) và mặt phẳng \(\left( {KMN} \right).\) Chứng minh rằng ba đường thẳng \(KH,MN,SB\) đồng quy.

Trong mặt phẳng \(\left( {ABC} \right)\) kéo dài \(EN\) cắt \(AB\) tại \(H.\)

\( \Rightarrow \left\{ \begin{array}{l}H \in \,EN \subset \left( {KMN} \right)\\H \in AB\end{array} \right. \Rightarrow AB \cap \left( {KMN} \right) = H\)

Xét ba mặt phẳng \(\left( {KMN} \right),\left( {SAB} \right),\left( {SBC} \right)\)

\(\left\{ \begin{array}{l}\left( {KMN} \right) \cap \left( {SAB} \right) = KH\\\left( {KMN} \right) \cap \left( {SBC} \right) = MN\\\left( {SBC} \right) \cap \left( {SAB} \right) = SB\end{array} \right.\) \( \Rightarrow KH//MN//SB\) hoặc \(KH,MN,SB\) đồng quy.

Mặt khác: \(\dfrac{{CN}}{{CB}} \ne \dfrac{{CM}}{{CS}}\left( {\dfrac{1}{2} \ne \dfrac{1}{3}} \right) \Rightarrow MN\) không song song với \(SB.\)

Vậy ba đường thẳng \(KH,MN,SB\) đồng quy.

Câu 5 (VD).

Phương pháp:

Sử dụng công thức \(C_n^k = C_n^{n - k},\forall n,k \in \mathbb{N}\left( {k \le n} \right)\)

Cách giải:

Ta có \(C_n^k = C_n^{n - k},\forall n,k \in \mathbb{N}\left( {k \le n} \right)\)

Do đó

\(C_n^3C_n^{n - 3} - 2C_n^3C_{n - 1}^2 + C_{n - 1}^2C_{n - 1}^{n - 3} = 14400\)

\( \Leftrightarrow {\left( {C_n^2} \right)^2} - 2C_n^3C_{n - 1}^2 + {\left( {C_{n - 1}^2} \right)^2} = 14400\)

\( \Leftrightarrow {\left( {C_n^3 - C_{n - 1}^2} \right)^2} = {120^2}\)

\( \Leftrightarrow \left[ \begin{array}{l}C_n^3 - C_{n - 1}^2 = 120\\C_n^3 - C_{n - 1}^2 =  - 120\end{array} \right.\)

+) \(C_n^3 - C_{n - 1}^2 = 120\) \( \Leftrightarrow \dfrac{{n!}}{{3!\left( {n - 3} \right)!}} - \dfrac{{\left( {n - 1} \right)!}}{{2!\left( {n - 3} \right)!}} = 120\) \( \Leftrightarrow \dfrac{{n\left( {n - 1} \right)\left( {n - 2} \right)}}{6} - \dfrac{{\left( {n - 1} \right)\left( {n - 2} \right)}}{2} = 120\)

\( \Leftrightarrow n\left( {{n^2} - 3n + 2} \right) - 3\left( {{n^2} - 3n + 2} \right) = 720\) \( \Leftrightarrow {n^3} - 6{n^2} + 11n - 726 = 0 \Leftrightarrow n = 11\)

+)\(C_n^3 - C_{n - 1}^2 =  - 120\) \( \Leftrightarrow \dfrac{{n!}}{{3!\left( {n - 3} \right)!}} - \dfrac{{\left( {n - 1} \right)!}}{{2!\left( {n - 3} \right)!}} =  - 120\)\( \Leftrightarrow \dfrac{{n\left( {n - 1} \right)\left( {n - 2} \right)}}{6} - \dfrac{{\left( {n - 1} \right)\left( {n - 2} \right)}}{2} =  - 120\)

\( \Leftrightarrow n\left( {{n^2} - 3n + 2} \right) - 3\left( {{n^2} - 3n + 2} \right) =  - 720\)\( \Leftrightarrow \left( {n - 1} \right)\left( {n - 2} \right)\left( {n - 3} \right) =  - 720\) (vô nghiệm do \(n \ge 3\))

\(T\left( x \right) = {\left( {8{x^6} - 36{x^3} - \dfrac{{27}}{{{x^3}}} + 54} \right)^{11}}\) \( = {\left[ {{{\left( {2{x^2} - \dfrac{3}{x}} \right)}^3}} \right]^{11}} = {\left( {2{x^2} - \dfrac{3}{x}} \right)^{33}}\)

Số hạng tổng quát trong khai triển trên là :

\(C_{33}^k{\left( {2{x^2}} \right)^{33 - k}} \cdot {\left( { - \dfrac{3}{x}} \right)^k} = C_{33}^k{.2^{33 - k}}.{\left( { - 3} \right)^k}.{x^{66 - 3k}}\)

Hệ số của số hạng chứa \({x^9}\) trong khai triển trên ứng với \(k\) là nghiệm của phương trình : \(66 - 3k = 9 \Leftrightarrow k = 19\)

Vậy hệ số cần tìm là \(C_{33}^{19}{.2^{14}}.{\left( { - 3} \right)^{19}}\)

HẾT