Đề kiểm tra 45 phút chương 1 phần Hình học 9 - Đề số 1

Đề bài

Câu 1 (3 điểm). Xét hình 59. Hãy chọn kết quả đúng

1. Giá trị của x là:

(A) \(\sqrt{10}\)                      (B) \(\sqrt {14} \) 

(C) \(\sqrt {20} \)                    (D) \(\sqrt {50} \)

2. Giá trị của y là:

(A) \(\sqrt {10} \)                    (B) \(\sqrt {14} \)

(C) \(\sqrt{20}\)                      (D) \(\sqrt {50} \)

3. Giá trị của z là:

(A) \(\sqrt {10} \)                    (B) \(\sqrt {14} \)

(C) \(\sqrt {20} \)                    (D) \(\sqrt {50} \)

Câu 2 (2 điểm). Cho tam giác ABC vuông tại A. vẽ hình và thiết lập các hệ thức tính các tỉ số lượng giác của góc B. từ đó, dựa vào tỉ số lượng giác của hai góc phụ nhau, hãy viết các hệ thức tính các tỉ số lượng giác của góc C.

Câu 3 (2 điểm). Dựng góc nhọn \(\beta \) , biết rằng \(\tan \alpha =\dfrac{4}{5}\)

Câu 4 (3 điểm). Giải tam giác vuông ABC, biết rằng \(\widehat{A}={{90}^{o}},\,\,AB=5,\,\,BC=7\) (kết quả về góc làm tròn đến phút, kết quả về cạnh làm tròn đến chữ số thập phân thứ ba).

LG câu 1

Phương pháp giải :

Vận dụng hệ thức về cạnh và đường cao trong tam giác vuông :

\({a^2} = ca';\,\)\({\rm{         }}{b^2} = cb';\)\({\rm{               }}{h^2} = a'b'\)

Lời giải :

1. Ta có : \({x^2} = 2.7 \Rightarrow x = \sqrt {14} \)

Chọn B.

2. Ta có : \({y^2} = 2.5 \Rightarrow y = \sqrt {10} \)

Chọn A.

3. Ta có : \({z^2} = 5.7 \Rightarrow z = \sqrt {35} \)

Chọn C.

LG câu 2

Phương pháp giải :

- Vận dụng kiến thức về tỉ số lượng giác :

 \(\sin \alpha  = \dfrac{{cạnh\,\,đối}}{{cạnh\,\,huyền}};\)\({\rm{    }}\cos \alpha  = \dfrac{{cạnh\,\,kề}}{{cạnh\,\,huyền}}\)

\(\tan \alpha  = \dfrac{{cạnh\,\,đối}}{{cạnh\,\,kề}};\)\({\rm{        }}\cot \alpha  = \dfrac{{cạnh\,\,kề}}{{cạnh\,\,đối}}\)

- Cho hai góc \(\alpha \) và \(\beta \) phụ nhau \(\left( {\alpha  + \beta  = {{90}^o}} \right)\). Ta có:

\(\sin \alpha  = \cos \beta ;\,\,\cos \alpha  = \sin \beta ;\)\(\tan \alpha  = \cot \beta ;\,\,\cot \alpha  = \tan \beta \)

Lời giải :

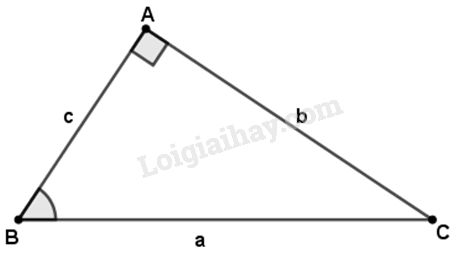
Tam giác vuông \(ABC\) có:

\(\sin B = \dfrac{b}{a};{\rm{ }}\cos B = \dfrac{c}{a};{\rm{ }}\tan B = \dfrac{b}{c};{\rm{ }}\cot B = \dfrac{c}{b}\)

Vì \(\widehat B\) và \(\widehat C\) là hai góc phụ nhau nên :

\(\sin C = \cos B = \dfrac{c}{a};\)\({\rm{      cos C = sin B = }}\dfrac{b}{a};\)

\(\tan C = \cot B = \dfrac{c}{b};\)\({\rm{        cot C =  tan B  = }}\dfrac{b}{c} \cdot \)

LG câu 3

Phương pháp giải :

Dựng tam giác vuông với góc nhọn \(\alpha \) có cạnh đối bằng \(4\) đơn vị độ dài; cạnh kề bằng \(5\) đơn vị độ dài.

Lời giải :

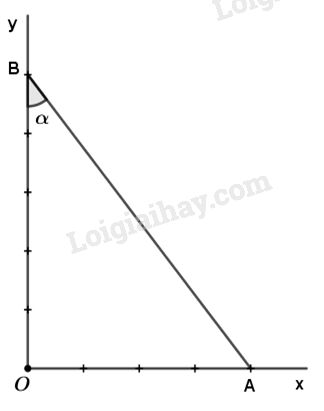
Dựng góc vuông \(xOy\). Lấy một đoạn thẳng làm đơn vị. Trên tia \(Ox\), lấy điểm \(A\) sao cho \(OA = 4.\) Trên tia \(Oy,\) lấy điểm B sao cho \(OB = 5.\) Góc \(\widehat {OBA}\) là góc \(\alpha \) cần dựng.

Thật vậy, trong tam giác vuông \(AOB,\) ta có :

\(\tan \alpha  = \tan \widehat {OBA} \)\(= \dfrac{{OA}}{{OB}} = \dfrac{4}{5}.\)

LG câu 4

Phương pháp giải :

- Áp dụng định lí Pi-ta-go tìm độ dài cạnh góc vuông còn  lại.

- Dùng tỉ số lượng giác tìm một trong hai góc nhọn.

- Áp dụng định lí tổng ba góc trong một tam giác hoặc tính chất hai góc nhọn phụ nhau trong tam giác vuông để tìm độ lớn của góc nhọn còn lại.

Lời giải :

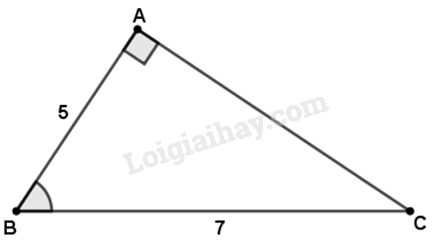
\(\Delta ABC\) vuông tại \(A,\) ta có :

\(AC = \sqrt {B{C^2} - A{B^2}}  = \sqrt {{7^2} - {5^2}}  \)\(= \sqrt {49 - 25}  = \sqrt {24}  \approx 4,899\) (định lí Pi-ta-go).

\(\sin C = \dfrac{{AB}}{{BC}} = \dfrac{5}{7} \)\(\approx 0,714 \Rightarrow \widehat C \approx {45^o}33'.\)

Theo định lí tổng ba góc trong một tam giác thì \(\widehat B = {90^o} - \widehat C \)\(\approx {90^o} - {45^o}33' = {44^o}27'.\)