Bài tập trắc nghiệm trang 84, 85, 86, 87 SBT hình học 11
Giải bài tập trắc nghiệm trang 84, 85, 86, 87 sách bài tập hình học 11
Chọn đáp án đúng:
2.51
Khẳng định nào sau đây đúng?
A. Nếu một mặt phẳng cắt một trong hai đường thẳng song song thì mặt phẳng đó sẽ cắt đường thẳng còn lại.
B. Hai mặt phẳng lần lượt đi qua hai đường thẳng song song thì cắt nhau theo một giao tuyến song song với một trong hai đường thẳng đó.
C. Nếu một đường thẳng cắt một trong hai đường thẳng song song thì đường thẳng đó sẽ cắt đường thẳng còn lại.
D. Hai mặt phẳng có một điểm chung thì cắt nhau theo một giao tuyến đi qua điểm chung nào đó.
Lời giải chi tiết:
Đáp án A: Nếu a // b và (α) cắt a thì (α) cắt b nên A đúng.
Đáp án B: sai vì có thể xảy ra hai mp song song.
Đáp án C: sai vì có thể chéo nhau.
Đáp án D: sai vì có thể hai mp đó trùng nhau.
Chọn đáp án: A
2.52
Khẳng định nào sau đây đúng?
A. Nếu hai mặt phẳng có một điểm chung thì chúng có một đường thẳng chung duy nhất.
B. Hai mặt phẳng có một điểm chung thì chúng còn vô số điểm chung khác nữa.
C. Tồn tại duy nhất một mặt phẳng đi qua 3 điểm phân biệt.
D. Tồn tại duy nhất một mặt phẳng đi qua 1 điểm và một đường thẳng cho trước
Lời giải chi tiết:
+ Khẳng định “ Nếu hai mặt phẳng có một điểm chung thì chúng có một đường thẳng chung duy nhất” là SAI, vì có thể hai mặt phẳng trùng nhau.
+ Khẳng định “Tồn tại duy nhất một mặt phẳng đi qua 3 điểm phân biệt” là SAI vì thiếu điều kiện ba điểm không thẳng hàng.
+ Khẳng định “Tồn tại duy nhất một mặt phẳng đi qua một điểm và một đường thẳng cho trước” SAI vì thiếu điều kiện điểm không nằm trên đường thẳng.
Chọn đáp án: B
2.53
Cho a ⊂ (P); b ⊂ (Q). Khẳng định nào sau đây đúng?
A. (P) // (Q) ⇒ a // b
B. a // b ⇒ (P) // (Q)
C. (P) // (Q) ⇒ a // (Q), b // (P)
D. a và b chéo nhau
Lời giải chi tiết:
Vì hai mặt phẳng song song thì không có điểm chung nên a và (Q) không có điểm chung, b và (P) không có điểm chung hay a // (Q), b // (P).
Chọn đáp án: C
2.54
Cho đường thẳng a và mặt phẳng (P) song song với nhau. Khi đó, số đường thẳng phân biệt nằm trong (P) và song song với a là
A. 0 B. 2 C. vô số D. 3
Lời giải chi tiết:
Ta có tính chất: “Đường thẳng a và mặt phẳng (P) song song với nhau khi trong mặt phẳng (P) tồn tại đường thẳng b song song với đường thẳng a”.
Do vậy chỉ cần qua một điểm bất kì nằm trong mặt phẳng (P) mà không thuộc đường thẳng b ta sẽ kẻ một đường thẳng c song song với b cũng nằm trong mặt phẳng (P), do đó đường thẳng vừa kẻ này sẽ song song với đường thẳng a.
Số điểm ở trong mặt phẳng (P) mà không thuộc đường thẳng b là vô số.
Vậy số đường thẳng chứa trong mặt phẳng (P) mà song song với đường thẳng a sẽ là vô số.
Chọn đáp án: C
2.55
Cho mặt phẳng (R) cắt hai mặt phẳng song song (P) và (Q) theo hai giao tuyến a và b. Khi đó, ta có
A. a và b song song hoặc trùng nhau
B. a và b cắt nhau
C. a và b trùng nhau
D. a và b song song
Lời giải chi tiết:
Ta có tính chất: “Một mặt phẳng thứ ba cắt hai mặt phẳng song song với nhau theo hai giao tuyến song song với nhau.”
Chọn đáp án: D
2.56
Khẳng định nào sau đây đúng?
A. Hai đường thẳng phân biệt không cắt nhau thì chéo nhau.
B. Hai đường thẳng phân biệt cùng nằm trong một mặt phẳng thì không chéo nhau.
C. Hai đường thẳng không có điểm chung thì song song với nhau.
D. Hai đường thẳng phân biệt lần lượt nằm trong hai mặt phẳng khác nhau thì chéo nhau.
Lời giải chi tiết:
+ Khẳng định “Hai đường thẳng phân biệt không cắt nhau thì chéo nhau” là SAI vì chúng có thể song song với nhau.
+ Khẳng định “Hai đường thẳng không có điểm chung thì song song với nhau” là SAI vì chúng có thể chéo nhau.
+ Khẳng định “Hai đường thẳng phân biệt lần lượt nằm trong hai mặt phẳng khác nhau thì chéo nhau” là SAI vì có thể hai đường thẳng này cùng thuộc một mặt phẳng thứ ba (nghĩa là chúng có thể song song).
Chọn đáp án: B
2.57
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AD và BC, G là trọng tâm tam giác BCD. Khi ấy giao tuyến của MG và mặt phẳng (ABC) là
A. điểm N.
B. điểm C.
C. Giao điểm của đường thẳng MG và đường thẳng BC.
D. Giao điểm của đường thẳng MG và đường thẳng AN.
Lời giải chi tiết:
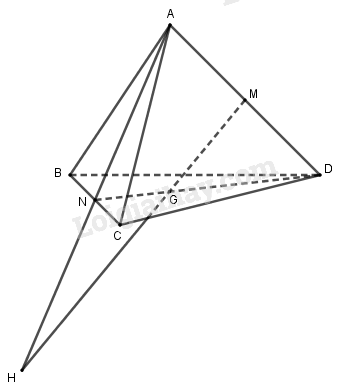
Ta có: \(AN = \left( {ADN} \right) \cap \left( {ABC} \right)\)
Trong \(\left( {ADN} \right)\), MG và AN không song song (vì \(\frac{{DM}}{{DA}} = \frac{1}{2} \ne \frac{2}{3} = \frac{{DG}}{{DN}}\)) nên gọi \(H = AN \cap MG\)
Khi đó \(\left\{ \begin{array}{l}H \in AN \subset \left( {ABC} \right)\\H \in MG\end{array} \right.\) \( \Rightarrow H = MG \cap \left( {ABC} \right)\)
Vậy giao điểm của MG và mặt phẳng (ABC) là giao điểm của MG với AN.
Chọn đáp án: D
2.58
Cho hình chóp S.ABCD, đáy ABCD là hình bình hành. Gọi G là trọng tâm tam giác SAD. Mặt phẳng (GBC) cắt SD tại E. Tỉ số SE / SD là
A. 1 B. 1/2
C. 2/3 D. 3/2
Lời giải chi tiết:
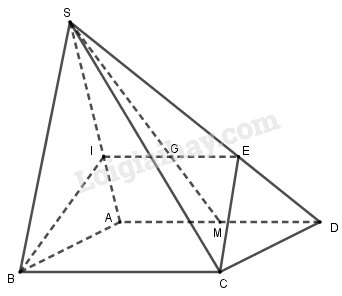
Mặt phẳng (SAD) và (GBC) có G là một điểm chung.
Mặt khác, (SAD) và (GBC) lần lượt chứa hai đường thẳng song song là AD và BC nên giao tuyến của chúng là đường thẳng qua G song song với AD.
Giao tuyến này cắt SD tại E. Gọi M là trung điểm AD, ta có GE//MD
\( \Rightarrow \frac{{SE}}{{SD}} = \frac{{SG}}{{SM}} = \frac{2}{3}\)
Chọn đáp án: C
2.59
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J lần lượt là trọng tâm các tam giác SAB, SAD. Lấy M là trung điểm CD. Khẳng định nào sau đây đúng?
A. IJ // (SBM) B. IJ // (SBD)
C. IJ // (SBC) D. IJ // (SCD)
Lời giải chi tiết:
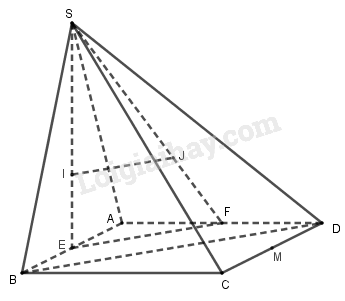
Gọi E, F lần lượt là trung điểm AB, AD.
Ta có: \(\frac{{SI}}{{SE}} = \frac{{SJ}}{{SF}} = \frac{2}{3}\) suy ra IJ // EF.
Mà EF // BD nên IJ // BD.
Do IJ không nằm trên (SBD), ta có: IJ // (SBD).
Chọn đáp án: B
2.60
Khẳng định nào sau đây đúng?
A. Nếu hai mặt phẳng (α) và (β) song song với nhau thì mọi đường thẳng nằm trong (α) đều song song với (β)
B. Nếu hai mặt phẳng (α) và (β) song song với nhau thì mọi đường thẳng nằm trong (α) đều song song với mọi đường thẳng trong (β)
C. Trong (α) có chứa hai đường thẳng phân biệt và hai đường thẳng này cùng song song với (β) thì (α) và (β) song song với nhau.
D. Qua một điểm nằm ngoài mặt phẳng (α) cho trước ta vẽ được một và chỉ một đường thẳng song song với mặt phẳng cho trước đó.
Lời giải chi tiết:
+ Khẳng định “Nếu hai mặt phẳng (α) và (β) song song với nhai thì mọi đường thẳng nằm trong (α) đều song song với mọi đường thẳng nằm trong (β)” là SAI vì hai đường thẳng có thể chéo nhau.
+ Khẳng định “Nếu (α) có chứa hai đường thẳng phân biệt và hai đường thẳng này cùng song song với (β) thì (α) và (β) song song” là SAI vì thiếu điều kiện hai đường thẳng đó cắt nhau.
+ Khẳng định “Qua một điểm nằm ngoài mặt phẳng cho trước ta vẽ được một là chỉ một đường thẳng song song với mặt phẳng cho trước đó” là SAI vì vẽ được vô số đường thẳng như vậy.
+ Khẳng định “Nếu hai mặt phẳng (α) và (β) song song với nhau thì mọi đường thẳng nằm trong (α) đều song song với (β)” là khẳng định đúng.
Chọn đáp án: A
2.61
Cho lăng trụ ABC.A'B'C'. Gọi G, G' lần lượt là trọng tâm của tam giác ABC, A'B'C'. M là điểm trên cạnh AC sao cho AM = 2MC. Khẳng định nào sau đây sai?
A. GG' // (ACC'A')
B. GG' // (ABB'A')
C. MG' // (BCC'B') ≠ ∅
D. (MGG') // (BCC'B')
Lời giải chi tiết:
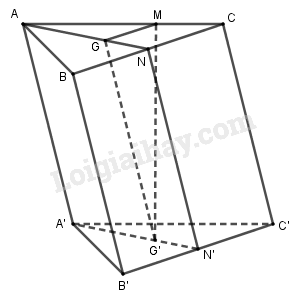
Gọi N, N’ là trung điểm của BC, B’C’.
Ta có ANN’A’ là hình bình hành (AA’//=NN’) nên GG’ // AA’.
Do đó GG’ // (ABB’A’), GG’ // (ACC’A’) nên A, B đều đúng.
Mặt khác: \(\frac{{AG}}{{AN}} = \frac{{AM}}{{AC}} = \frac{2}{3}\) nên GM // CN\( \Rightarrow GM//\left( {BCC'B'} \right)\)
Mà \(GG'//\left( {BCC'B'} \right)\) nên (MGG’) // (BCCB’).
Do vậy khẳng định “Đường thẳng MG’ cắt mặt phẳng (BCC’B’) là khẳng định SAI.
Chọn đáp án: C
2.62
Cho mặt phẳng (P) và đường thẳng d ⊂ (P). Khẳng định nào sau đây đúng?
A. Nếu 3 điểm A, B, C cùng thuộc (P) và A, B, C thẳng hàng thì A, B, C ∈ d.
B. Nếu A ∉ d thì A ∉ (P).
C. Nếu A ∈ (P) thì A ∉ d.
D. ∀A, A ∈ d ⇒ A ∈ (P)
Lời giải chi tiết:
+ Ta có tính chất: “Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm nằm trên đường thẳng đó đều nằm trên mặt phẳng đó”.
+ Khẳng định “Nếu A ∉ d thì A ∉ (P)” là SAI vì có thể vẫn thuộc (P) nhưng không nằm trên d.
Chọn đáp án: D
2.63
Khẳng định nào sau đây sai?
A. Qua một điểm và một đường thẳng không chứa điểm đó có duy nhất một mặt phẳng.
B. Qua hai đường thẳng cắt nhau có duy nhất một mặt phẳng.
C. Qua hai đường thẳng song song có duy nhất một mặt phẳng.
D. Qua hai đường thẳng không chéo nhau có duy nhất một mặt phẳng.
Lời giải chi tiết:
Đáp án A, B, C đúng theo các cách xác định mặt phẳng.
Đáp án D: Nếu hai đường thẳng trùng nhau thì có vô số mặt phẳng nên D sai.
Chọn đáp án: D
2.64
Cho năm điểm A, B, C, D, E sao cho không có bốn điểm nào cùng nằm trên một mặt phẳng. Số hình tứ diện có các đỉnh lấy từ năm điểm đã cho là
A. 5 B. 6 C. 3 D. 4
Lời giải chi tiết:
Lấy bốn điểm trong năm điểm có: C54 = 5 cách (vì bốn điểm trong năm điểm đều tạo thành tứ diện).
Chọn đáp án: A.
2.65
Cho tứ diện ABCD. Trên các cạnh AB, AD lần lượt lấy các điểm M, N sao cho \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AD}} = \frac{1}{3}\). Gọi P, Q lần lượt là trung điểm các cạnh CD, CB.
Khẳng định nào sau đây đúng?
A. Bốn điểm M, N, P, Q không đồng phẳng.
B. Tứ giác MNPQ là hình bình hành.
C. Tứ giác MNPQ là hình thang.
D. Tứ giác MNPQ không có các cặp cạnh đối nào song song.
Lời giải chi tiết:
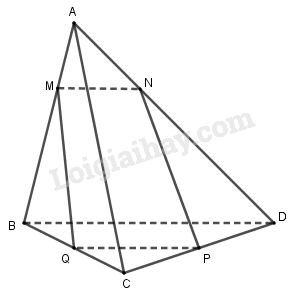
Vì \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AD}} = \frac{1}{3}\) nên MN // BD
Tam giác BCD có PQ là đường trung bình nên PQ // BD và \(PQ = \frac{1}{2}BD\)
Do đó MN//PQ và MN < PQ nên tứ giác MNPQ là một hình thang.
Chọn đáp án: D
2.66
Cho tứ diện đều ABCD. Một mặt phẳng (α) qua trung điểm của cạnh AB và lần lượt song song với AC và BD cắt tứ diện trên theo thiết diện là
A. hình chữ nhật. B. hình vuông.
C. hình thoi. D. hình thang cân.
Lời giải chi tiết:
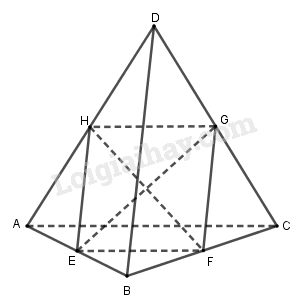
Gọi E là trung điểm AB. Ta có \(E \in \left( {ABC} \right) \cap \left( \alpha \right)\).
\(\left\{ \begin{array}{l}AC \subset \left( {ABC} \right)\\AC//\left( \alpha \right)\\\left( \alpha \right) \cap \left( {ABC} \right) = Ex\end{array} \right.\) \( \Rightarrow Ex//AC\)
Trong mp(ABC), kẻ \(Ex//AC\) cắt BC tại F nên F là trung điểm BC.
Ta có: \(\left\{ \begin{array}{l}F \in \left( \alpha \right) \cap \left( {BCD} \right)\\BD \subset \left( {BCD} \right)\\BD//\left( \alpha \right)\\\left( \alpha \right) \cap \left( {BCD} \right) = Fy\end{array} \right.\) \( \Rightarrow Fy//BD\)
Trong mp(BCD), kẻ \(Fy//BD\) cắt \(DC\) tại G, khi đó G là trung điểm DC.
Ta có: \(\left\{ \begin{array}{l}G \in \left( \alpha \right) \cap \left( {ACD} \right)\\AC \subset \left( {ACD} \right)\\AC//\left( \alpha \right)\\\left( \alpha \right) \cap \left( {ACD} \right) = Gz\end{array} \right.\) \( \Rightarrow Gz//AC\)
Trong mp(ACD), kẻ \(Gz//AC\) cắt \(DA\) tại H, khi đó H là trung điểm DA.
Do đó
\(\begin{array}{l}EF = GH = \frac{1}{2}AC\\FG = HE = \frac{1}{2}BD\end{array}\)
Mà AC=BD do hình tứ diện đều nên \(EF = GH = FG = HE\) hay EFGH là hình thoi.
Xét hai tam giác đều ABC và DBC bằng nhau (c-c-c) nên AF=DF (hai đường trung tuyến tương ứng)
Do đó tam giác ADF cân tại F.
Xét hai tam giác đều DAB và CAB bằng nhau (c-c-c) nên DE=CE (hai đường trung tuyến tương ứng)
Do đó tam giác ADF cân tại F.
Mà CE=AF nên AF=DF=DE=DE.
Suy ra hai tam giác DAF và DCE bằng nhau (c-c-c)
\( \Rightarrow HF = EG\) (hia trung tuyến tương ứng)
Thiết diện EFGH là một hình thoi có hai đường chéo bằng nhau nên nó là một hình vuông.
Chọn đáp án: B
2.67
Cho hai hình bình hành ABCD và ABEF lần lượt có tâm O1, O2 và không cùng nằm trong một mặt phẳng. Khẳng định nào sau đây sai?
A. O1O2 song song với mặt phẳng (BCE).
B. O1O2 song song với mặt phẳng (BDE).
C. O1O2 song song với mặt phẳng (ADF).
D. O1O2 song song với mặt phẳng (CDE).
Lời giải chi tiết:
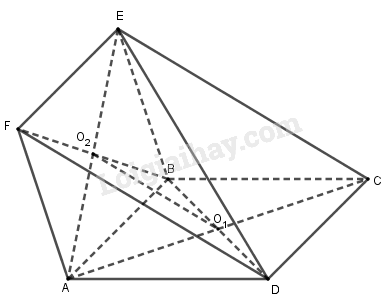
\({O_1}{O_2}\) là đường trung bình tam giác ACE nên \({O_1}{O_2}//CE \Rightarrow {O_1}{O_2}//\left( {BCE} \right)\) nên A đúng.
Vì O1O2 ∩ (BDE) = O1 nên B sai.
\({O_1}{O_2}\) là đường trung bình tam giác BDF nên \({O_1}{O_2}//DF \Rightarrow {O_1}{O_2}//\left( {ADF} \right)\) nên C đúng.
Lại có \({O_1}{O_2}//CE \Rightarrow {O_1}{O_2}//\left( {CDE} \right)\) nên D đúng.
Chọn đáp án: B
2.68
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, I lần lượt là trung điểm của các cạnh AB, SC. Mặt phẳng (α) qua M song song với mặt phẳng (BID) sẽ cắt hình chóp theo thiết diện là
A. hình tam giác B. hình lục giác
C. hình tứ giác D. hình ngũ giác
Lời giải chi tiết:
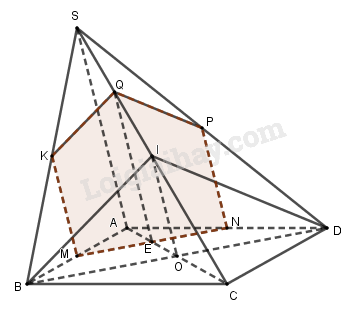
+) Trong (ABCD), kẻ MN//BD (\(N \in AD\))
Gọi O, E lần lượt là giao điểm của BD, MN với AC.
+) Ta có: \(\left\{ \begin{array}{l}\left( \alpha \right)//\left( {BID} \right)\\\left( {SAC} \right) \cap \left( {BID} \right) = IO\\\left( \alpha \right) \cap \left( {SAC} \right) = Ex\end{array} \right.\) \( \Rightarrow Ex//IO\)
Trong mp(SAC), kẻ tia Ex//IO cắt SC tại Q.
+) Ta có: \(\left\{ \begin{array}{l}\left( \alpha \right)//\left( {BID} \right)\\\left( {SBC} \right) \cap \left( {BID} \right) = IB\\\left( \alpha \right) \cap \left( {SBC} \right) = Qy\end{array} \right.\) \( \Rightarrow Qy//IB\)
Trong mp(SBC), kẻ Qy//IB cắt SB tại K.
+) Ta có: \(\left\{ \begin{array}{l}\left( \alpha \right)//\left( {BID} \right)\\\left( {SDC} \right) \cap \left( {BID} \right) = ID\\\left( \alpha \right) \cap \left( {SDC} \right) = Qz\end{array} \right.\) \( \Rightarrow Qz//ID\)
Trong mp(SDC), kẻ Qz//ID cắt SD tại P.
Khi đó
\(\begin{array}{l}\left( \alpha \right) \cap \left( {ABCD} \right) = MN\\\left( \alpha \right) \cap \left( {SAD} \right) = NP\\\left( \alpha \right) \cap \left( {SDC} \right) = PQ\\\left( \alpha \right) \cap \left( {SBC} \right) = QK\\\left( \alpha \right) \cap \left( {SAA} \right) = KM\end{array}\)
Do đó thiết diện là ngũ giác MNPQK.
Chọn đáp án: B
2.69
Trong mặt phẳng (α), cho tứ giác ABCD có O là giao điểm của AC và BD. S nằm ngoài (ABCD). Giao tuyến của (SAC) và (SBD) là
A. BD B. AC C. SO D. SC
Lời giải chi tiết:
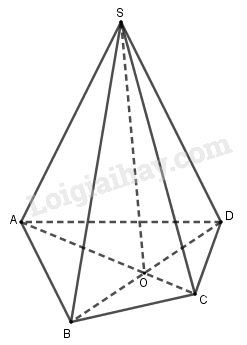
Ta có S ∈ (SAC) ∩ (SBD) (1)
Mà O ∈ AC ⊂(SAC) và O ∈ BD ⊂(SBD)
⇒ O ∈ (SAC) ∩ (SBD) (2)
Từ (1) và (2) suy ra (SAC) ∩ (SBD) = SO.
Chọn đáp án: C
2.70
Cho hình chóp S.ABCD với I = AB ∩ CD. Giao tuyến của (SAB) và (SCD) là
A. SB B. SI C. SC D. BC
Lời giải chi tiết:
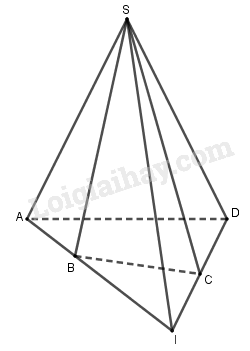
Ta có S ∈ (SAB) ∩ (SCD) (1)
Mà I∈ AB ⊂(SAB) và I∈ CD ⊂(SCD)
⇒ I ∈ (SAB) ∩ (SCD) (2)
Từ (1) và (2) suy ra (SAB) ∩ (SCD) = SI.
Chọn đáp án: B
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài tập trắc nghiệm trang 84, 85, 86, 87 SBT hình học 11 timdapan.com"







