Bài tập trắc nghiệm trang 180, 181 SBT Đại số 10

Chọn đáp án đúng:

6.7

Số đo của góc 9π/5 đổi ra độ là

    A. 266^ο          B. 258^ο

    C. 324^ο          D. 374^ο

Phương pháp giải:

Sử dụng công thức \(n\,rad = {\left( {\dfrac{{180n}}{\pi }} \right)^0}\)

Lời giải chi tiết:

Ước lượng: Ta có 270^o = 3π/2 < 9π/5 < 2π = 360^o nên các phương án A, B, D bị loại.

Cách khác:

Tính trực tiếp \(\dfrac{{9\pi }}{5} = {\left( {\dfrac{{\dfrac{{9\pi }}{5}.180}}{\pi }} \right)^0} = {324^0}\)

Đáp án: C

6.8

Số đo của cung 37^ο15' đổi ra radian (lấy đến ba chữ số thập phân) là

    A. 0,652          B. 0,514

    C. 0,482          D. 0,793

Phương pháp giải:

Tính trực tiếp sử dụng công thức \({n^0} = \dfrac{{n\pi }}{{180}}\left( {rad} \right)\)

Chú ý rằng 37^o15’ phải đổi ra thập phân.

Lời giải chi tiết:

Cách 1. Ước lượng:

Ta có \({30^0} < {37^0}15' < {45^0}\) \( \Rightarrow \dfrac{\pi }{6} < {37^0}15' < \dfrac{\pi }{4}\)

Mà \(\dfrac{\pi }{6} \approx \dfrac{{3,14}}{6}\) = 0,523 và \(\dfrac{\pi }{4} \approx 0,785\) nên \(0,523 < {37^0}15' < 0,785\)

Các phương án B,C, D bị loại.

Vậy đáp án là A.

Cách khác:

\(15' = {\left( {\dfrac{{15}}{{60}}} \right)^0} = 0,{25^0}\)

⇒ 37^o15’ = 37,25^o\( = \dfrac{{37,25\pi }}{{180}} = 0,652\left( {rad} \right)\)

Đáp án: A

6.9

Cho hình ngũ giác đều ABCDE (các đỉnh lấy theo thứ tự đó và thuận chiều quay của kim đồng hồ) nội tiếp trong đường tròn lượng giác. Số đo bằng radian của các cung lượng giác AB, DA, EA lần lượt là:

A. \(\dfrac{\pi }{5}; - \dfrac{{3\pi }}{5}; - \dfrac{{4\pi }}{5}\)

B. \( - \dfrac{{2\pi }}{5};\dfrac{{6\pi }}{5};\dfrac{{8\pi }}{5}\)

C. \( - \dfrac{{2\pi }}{5};\dfrac{{6\pi }}{5}; - \dfrac{{8\pi }}{5}\)

D. \(\dfrac{\pi }{5};\dfrac{{3\pi }}{5};\dfrac{{4\pi }}{5}\)

Lời giải chi tiết:

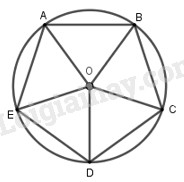
Cách 1: Suy luận

Cung AB ngược hướng dương của đường tròn lượng giác nên có số đo âm, còn cung DA và EA có số đo dương. Do đó các phương án A, C, D bị loại.

Cách 2: Tính trực tiếp \(sdAB =  - \dfrac{{2\pi }}{5},\) \(sdDA = 3.\dfrac{{2\pi }}{5} = \dfrac{{6\pi }}{5},\) \(sdEA = 4.\dfrac{{2\pi }}{5} = \dfrac{{8\pi }}{5}\)

Đáp án: B

6.10

Một đường tròn có đường kính 36 cm. Độ dài của cung trên đường tròn đó có số đo 20^ο là

    A. 7,2cm          B. 4,6cm

    C. 6,8cm          D. 6,3cm

Phương pháp giải:

Để tính độ dài l của một cung có số đo α radian trên đường tròn bán kính R ta áp dụng công thức: l = Rα

Lời giải chi tiết:

Đổi số đo 20^o thành radian ta được:

20 x 0,0175 = 0,35

Với bán kính R = 36/2 = 18 ta có độ dài l là: 18 x 0,35 = 6,3 (cm).

Đáp án: D

6.11

Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM = -70^ο với A(1; 0). Gọi M₁ là điểm đối xứng của M qua đường phân giác của góc phần tư thứ I. Số đo của cung lượng giác AM₁ là

    A. -150^ο          B. 220^ο

    C. 160^ο          D. -160^ο

Lời giải chi tiết:

Cách 1. Suy luận.

Điểm M nằm ở góc phần tư thứ IV nên điểm M₁ nằm ở góc phần tư thứ hai. Số đo AM₁ dương nên hai phương án A, D bị loại. Mặt khác sđ AM₁ < 180^o nên phương án B bị loại.

Vậy đáp án là C.

Cách 2. Tính trực tiếp.

Gọi B là giao điểm của đường phân giác góc xOy với đường tròn. Ta có

Sđ AB = 45^o, sđ MA = 70^o

Suy ra sđ MB = 115^o.

Mà sđ BM₁ = sđ MB nên sđ AM₁ = 45^o + 115^o = 160^o.

Đáp án: C

6.12

Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM = α, π < α < 3π/2, A(1; 0). Gọi M₂ là điểm đối xứng với M qua trục Ox. Số đo của cung AM₂ là

A. α - π + k2π, k ∈ Z

B. π - α + k2π, k ∈ Z

C. 2π - α + k2π, k ∈ Z

D. 3π/2 - α + k2π, k ∈ Z

Lời giải chi tiết:

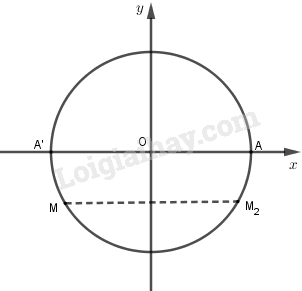
Ta có

Cung AM₂ = cung AA’ + cung A’ M₂

Suy ra

Sđ AM₂ = sđ AA’ + sđ A’ M₂

= sđ AA’ + sđ MA = π + (-α) + k2π, k ∈ Z.

Vậy đáp án là B.

6.13

Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM = α, π/2 < α < π, A(1; 0). Gọi M₂ là điểm đối xứng với M qua trục Ox. Số đo của cung AM₃ là

A. π - α + k2π, k ∈ Z

B. α + π/2 + k2π, k ∈ Z

C. α - π + k2π, k ∈ Z

D. -α + k2π, k ∈ Z

Lời giải chi tiết:

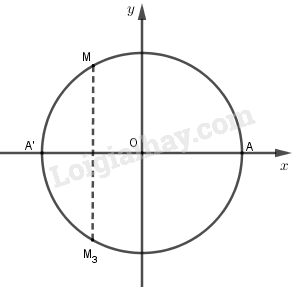
Ta có

Sđ AM₃ = - sđ AM = - α + k2π, k ∈ Z.

Đáp án: D

6.14

Trên đường tròn lượng giác cho cung lượng giác AM có số đo là -6,32, với A(1; 0). Xác định xem điểm cuối M nằm trong góc phần tư vào của đường tròn lượng giác.

    A. Góc phần tư thứ I

    B. Góc phần tư thứ II

    C. Góc phần tư thứ III

    D. Góc phần tư thứ IV

Lời giải chi tiết:

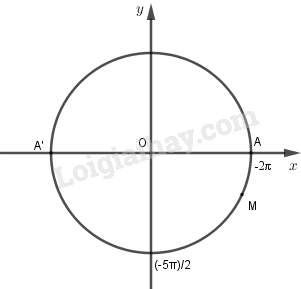
-π = -3,14; -2π = -6,28; (-5π)/2 = -7,85.

Vậy (-5π)/2 < -6,32 < -2π.

Do đó điểm M nằm ở góc phần tư thứ IV.

Cách khác:

Các cung có điểm đầu và điểm cuối trùng nhau thì hơn kém nhau \(k2\pi ,\) do đó điểm M trùng với điểm cuối cung có số đo \( - 6,32 + 2\pi  =  - 0,04\).

Điểm này nằm ở góc phần tư thứ IV hay M cũng nằm ở góc phần tư thứ IV.

Đáp án: D