Giải bài tập 5 trang 27 SGK Toán 12 tập 2 - Chân trời sáng tạo
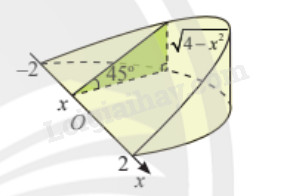
Khi cắt một vật thể hình chiếc nêm bởi mặt phẳng vuông góc với trục (Ox) tại điểm có hoành độ (x) (left( { - 2 le x le 2} right)), mặt cắt là tam giác vuông có một góc ({45^o}) và độ dài một cạnh góc vuông là (sqrt {4 - {x^2}} ) (dm). Tính thể tích của vật thể.
Đề bài
Khi cắt một vật thể hình chiếc nêm bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\) \(\left( { - 2 \le x \le 2} \right)\), mặt cắt là tam giác vuông có một góc \({45^o}\) và độ dài một cạnh góc vuông là \(\sqrt {4 - {x^2}} \) (dm). Tính thể tích của vật thể.
Phương pháp giải - Xem chi tiết
Tính diện tích mặt cắt \(S\left( x \right)\), sau đó tính thể tích vật thể bằng công thức \(V = \int\limits_a^b {S\left( x \right)dx} \).
Lời giải chi tiết
Vì mặt cắt là một tam giác vuông có một góc \({45^o}\), nên mặt cắt là tam giác vuông cân. Do đó diện tích mặt cắt là \(S\left( x \right) = \frac{{{{\left( {\sqrt {4 - {x^2}} } \right)}^2}}}{2} = \frac{{4 - {x^2}}}{2}\).
Thể tích vật thể là:
\(V = \int\limits_{ - 2}^2 {\frac{{4 - {x^2}}}{2}dx} = \frac{1}{2}\int\limits_{ - 2}^2 {\left( {4 - {x^2}} \right)dx} = \frac{1}{2}\left. {\left( {4x - \frac{{{x^3}}}{3}} \right)} \right|_{ - 2}^2 = \frac{{16}}{3}\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài tập 5 trang 27 SGK Toán 12 tập 2 - Chân trời sáng tạo timdapan.com"







