Giải bài tập 3 trang 36 SGK Toán 12 tập 1 - Chân trời sáng tạo

Đề bài

Khảo sát và vẽ đồ thị của các hàm số sau:

a) \(y = 3 + \frac{1}{x}\)

b) \(y = \frac{{x - 3}}{{1 - x}}\)

Lời giải chi tiết

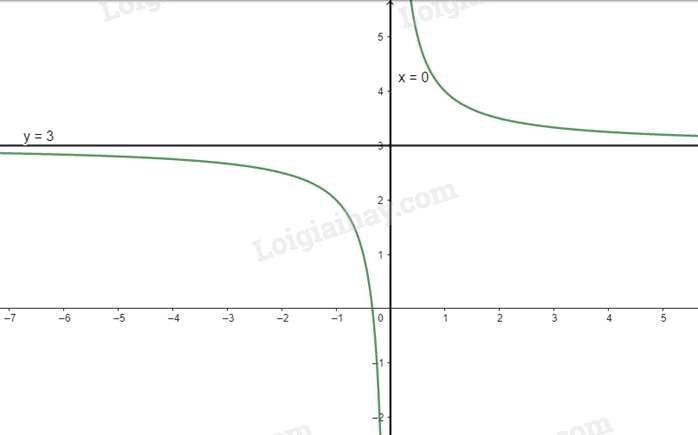
a) \(y = 3 + \frac{1}{x}\)

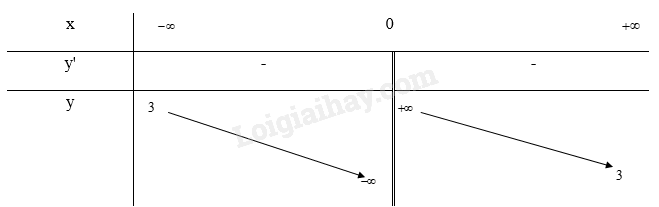
Tập xác định: \(D = \mathbb{R}\backslash \{ 0\} \)

• Chiều biến thiên:

\(y' =  - \frac{1}{{{x^2}}} < 0\forall x \in D\) nên hàm số nghịch biến trên D

• Tiệm cận:

\(\mathop {\lim }\limits_{x \to  + \infty } y = \mathop {\lim }\limits_{x \to  + \infty } (3 + \frac{1}{x}) = 3;\mathop {\lim }\limits_{x \to  - \infty } y = \mathop {\lim }\limits_{x \to  - \infty } (3 + \frac{1}{x}) = 3\) nên y = 3 là tiệm cận ngang của đồ thị hàm số

\(\mathop {\lim }\limits_{x \to {0^ + }} y = \mathop {\lim }\limits_{x \to {0^ + }} (3 + \frac{1}{x}) =  + \infty ;\mathop {\lim }\limits_{x \to {0^ - }} y = \mathop {\lim }\limits_{x \to {0^ - }} (3 + \frac{1}{x}) =  - \infty \) nên x = 0 là tiệm cận đứng của đồ thị hàm số

• Bảng biến thiên:

Ta có: \(y = 0 \Leftrightarrow 3 + \frac{1}{x} = 0 \Leftrightarrow x =  - \frac{1}{3}\)

Vậy đồ thị của hàm số giao với trục Ox tại điểm (\( - \frac{1}{3}\); 0)

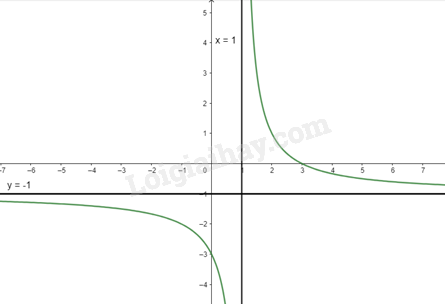
b) \(y = \frac{{x - 3}}{{1 - x}}\)

Tập xác định: \(D = \mathbb{R}\backslash \{ 1\} \)

• Chiều biến thiên:

\(y' = \frac{{ - 2}}{{{{(1 - x)}^2}}} < 0\forall x \in D\) nên hàm số nghịch biến trên D

• Tiệm cận:

\(\mathop {\lim }\limits_{x \to  + \infty } y = \mathop {\lim }\limits_{x \to  + \infty } \frac{{x - 3}}{{1 - x}} =  - 1\mathop {\lim }\limits_{x \to  - \infty } y = \mathop {\lim }\limits_{x \to  - \infty } \frac{{x - 3}}{{1 - x}} =  - 1\) nên y = -1 là tiệm cận ngang của đồ thị hàm số

\(\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{x - 3}}{{1 - x}} =  + \infty ;\mathop {\lim }\limits_{x \to {1^ - }} y = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{x - 3}}{{1 - x}} =  - \infty \) nên x = 1 là tiệm cận đứng của đồ thị hàm số

• Bảng biến thiên:

Khi x = 0 thì y = -3 nên (0; -3) là giao của đồ thị hàm số với trục Oy

Ta có: \(y = 0 \Leftrightarrow \frac{{x - 3}}{{1 - x}} = 0 \Leftrightarrow x = 3\)

Vậy đồ thị của hàm số giao với trục Ox tại điểm (3; 0)