Giải bài tập 2 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau: a) \(y = {x^3} - 12x + 1\) trên đoạn [-1;3] b) \(y = - {x^3} + 24{x^2} - 180x + 400\) trên đoạn [3;11] c) \(y = \frac{{2x + 1}}{{x - 2}}\) trên đoạn [3;7] d) \(y = \sin 2x\) trên đoạn \([0;\frac{{7\pi }}{{12}}]\)
Đề bài
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) \(y = {x^3} - 12x + 1\) trên đoạn [-1;3]
b) \(y = - {x^3} + 24{x^2} - 180x + 400\) trên đoạn [3;11]
c) \(y = \frac{{2x + 1}}{{x - 2}}\) trên đoạn [3;7]
d) \(y = \sin 2x\) trên đoạn \([0;\frac{{7\pi }}{{12}}]\)
Phương pháp giải - Xem chi tiết
Tìm đạo hàm, lập bảng biến thiên và xác định giá trị lớn nhất, giá trị nhỏ nhất của hàm số
Lời giải chi tiết
a) Xét \(y = {x^3} - 12x + 1\) trên đoạn [-1;3]
\(y' = 3{x^2} - 12 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = - 2(loai)\end{array} \right.\)
Bảng biến thiên:
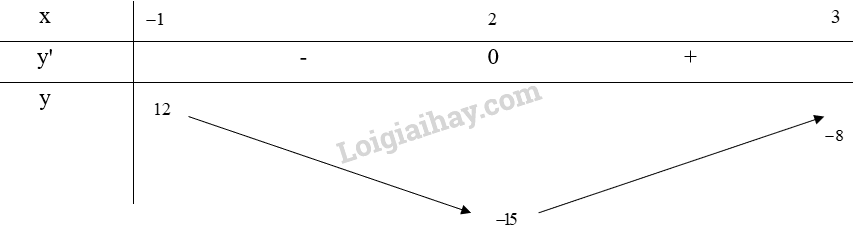
Từ bảng biến thiên, ta thấy \(\mathop {\max }\limits_{[ - 1;3]} y = y( - 1) = 12\) và \(\mathop {\min }\limits_{[ - 1;3]} y = y(2) = - 15\)
b) Xét \(y = - {x^3} + 24{x^2} - 180x + 400\) trên đoạn [3;11]
\(y' = - 3{x^2} + 48x - 180 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 10\\x = 6\end{array} \right.\)
Bảng biến thiên:

Từ bảng biến thiên, ta thấy \(\mathop {\max }\limits_{[3;11]} y = y(3) = 49\) và \(\mathop {\min }\limits_{[3;11]} y = y(6) = - 32\)
c) Xét \(y = \frac{{2x + 1}}{{x - 2}}\) trên đoạn [3;7]
\(y' = \frac{{ - 5}}{{{{(x - 2)}^2}}} < 0\forall x \in [3;7]\)
Bảng biến thiên:
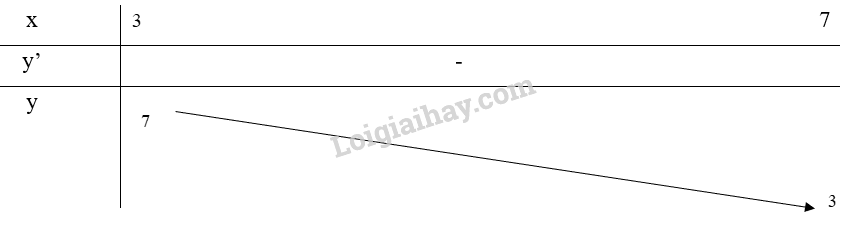
Từ bảng biến thiên, ta thấy \(\mathop {\max }\limits_{[3;7]} y = y(3) = 7\) và \(\mathop {\min }\limits_{[3;7]} y = y(7) = 3\)
d) Xét \(y = \sin 2x\) trên đoạn \([0;\frac{{7\pi }}{{12}}]\)
\(y' = 2\cos 2x = 0 \Leftrightarrow 2x = \frac{\pi }{2} + k\pi \Leftrightarrow x = \frac{\pi }{4} + \frac{{k\pi }}{2}(k \in \mathbb{Z})\)
Ta có: \(x \in [0;\frac{{7\pi }}{{12}}] \Rightarrow k = 0 \Rightarrow x = \frac{\pi }{4}\)
Bảng biến thiên:
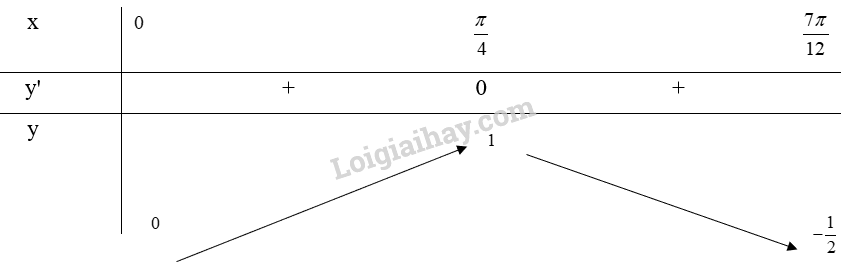
Từ bảng biến thiên, ta thấy \(\mathop {\max }\limits_{[0;\frac{{7\pi }}{{12}}]} y = y(\frac{\pi }{4}) = 1\) và \(\mathop {\min }\limits_{[0;\frac{{7\pi }}{{12}}]} y = y(\frac{{7\pi }}{{12}}) = - \frac{1}{2}\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài tập 2 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo timdapan.com"







