Giải bài tập 10 trang 128 SGK Toán 9 tập 2 - Kết nối tri thức
Cho tam giác ABC vuông tại B có góc \(\widehat A = {30^o},AB = 6cm\). Vẽ tia Bt sao cho \(\widehat {tBC} = {30^o}\), cắt tia AC ở D (C nằm giữa A và D). a) Chứng minh tam giác ABD cân tại B. b) Tính khoảng cách từ D đến đường thẳng AB.
Đề bài
Cho tam giác ABC vuông tại B có góc \(\widehat A = {30^o},AB = 6cm\). Vẽ tia Bt sao cho \(\widehat {tBC} = {30^o}\), cắt tia AC ở D (C nằm giữa A và D).
a) Chứng minh tam giác ABD cân tại B.
b) Tính khoảng cách từ D đến đường thẳng AB.
Phương pháp giải - Xem chi tiết
a) + Tính được \(\widehat {DBA} = \widehat {DBC} + \widehat {CBA} = {120^o}\).
+ Tính được \(\widehat {BDA} = {30^o}\) nên tam giác ABD cân tại B.
b) + \(BD = AB = 6cm\).
+ Kẻ DE vuông góc với AB tại E. Khi đó, DE là khoảng cách từ D đến đường thẳng AB.
+ \(\widehat {DBE} = {180^o} - \widehat {DBA} = {60^o}\).
+ Tam giác BED vuông tại E nên \(ED = BD.\sin \widehat {DBE}\).
Lời giải chi tiết
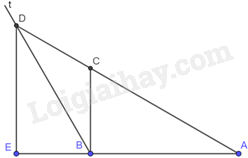
a) \(\Delta \)ABC vuông tại B nên \(\widehat {CBA} = {90^o}\). Ta có: \(\widehat {DBA} = \widehat {DBC} + \widehat {CBA} = {30^o} + {90^o} = {120^o}\)
\(\Delta \)DBC có: \(\widehat {BDA} = {180^o} - \widehat {DBA} - \widehat A = {180^o} - {120^o} - {30^o} = {30^o}\). Do đó, \(\widehat {BDA} = \widehat A\) nên \(\Delta \)ABD cân tại B.
b) Vì \(\Delta \)ABD cân tại B nên \(BD = AB = 6cm\).
Kẻ DE vuông góc với AB tại E. Khi đó, DE là khoảng cách từ D đến đường thẳng AB.
Ta có: \(\widehat {DBE} = {180^o} - \widehat {DBA} = {180^o} - {120^o} = {60^o}\).
\(\Delta \)BED vuông tại E nên \(ED = BD.\sin \widehat {DBE} = 6.\sin {60^o} = 6.\frac{{\sqrt 3 }}{2} = 3\sqrt 3 \left( {cm} \right)\)
Vậy khoảng cách từ D đến đường thẳng AB bằng \(3\sqrt 3 \)cm.
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài tập 10 trang 128 SGK Toán 9 tập 2 - Kết nối tri thức timdapan.com"







