Bài II.9, II.10, II.11 trang 39,40 SBT Vật lí 10

II.9.

Hai đội A và B chơi trò chơi kéo co. Nếu đội A kéo dây bằng một lực có độ lớn bằng 250 N, thì đội B kéo dây bằng một lực có độ lớn bằng bao nhiêu ? Xét hai trường hợp :

a) hai đội hoà ;

b) đội A thắng ;

Phương pháp giải:

Sử dụng định luật III Niu tơn: Trong mọi trường hợp, khi vật A tác dụng lên vật B một lực, thì vật B cũng tác dụng lại vật A một lực. Hai lực này có cùng giá, cùng độ lớn nhưng ngược chiều

Lời giải chi tiết:

Theo định luật III Niu-tơn, ở cả hai trường hợp, Jực của đội A kéo dây và lực của đội B kéo dây đều là cặp ^ulực và phản lực", do đó đều có độ lớn bằng nhau, tức là bằng 250 N.

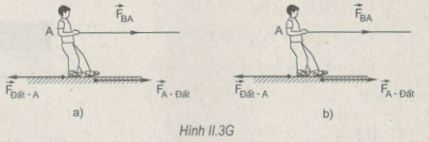
a) Hai đội hoà là vì hai đội cùng đạp chân vào mặt đất với một lực có độ lớn bằng nhau. Theo định luật II Niu-tơn, phản lực mà mặt đất tác dụng vào hai đội cũng có độ lớn bằng nhau. Nếu xét từng đội, thì lực kéo của đối phương phương và phản lực của mặt đất tác dụng vào mỗi đội cân bằng nhau làm mỗi đội đứng yên (H.II.3Ga).

b) Đội A thắng là vì đội A đạp chân vào mặt đất với một lực lớn hơn. Theo định luật III, mặt đất tác dụng lại đội A một lực lớn hơn lực mà đội B kéo đội A, làm đội A thu gia tốc và chuyển động kéo theo đội B chuyển động về phía mình (H.II.3Gb).

II.10.

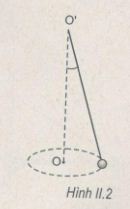
Một hòn đá được treo vào một điểm cố định bằng một sợi dây dài 1,00 m. Quay dây sao cho chất điểm chuyển động tròn đều trong mặt phẳng nằm ngang và thực hiện được 30 vòng trong một phút (H_.II.2). Lấy g = 9,8 m/s².

a) Tính góc nghiêng của dây so với phương thẳng đứng.

b) Hòn đá đang chuyển động thì dây bị đứt và hòn đá bị văng đi từ độ cao 1,00 m so với mặt đất. Tính quãng  đường mà vật đi được theo phương ngang kể từ khi dây đứt.

Phương pháp giải:

Áp dụng công thức:

- Công thức tính tốc độ góc \(\omega  = 2\pi f\)

- Công thức tính tốc độ dài \(v = \omega r\)

- Công thức tính thời gian rơi \(t = \sqrt {\dfrac{{2h}}{g}} \)

- Công thức tính sin, tan trong tam giác vuông

Lời giải chi tiết:

\(\omega = 2\pi f = \displaystyle{{6,28.30} \over {60}} = 3,14(rad/s)\)

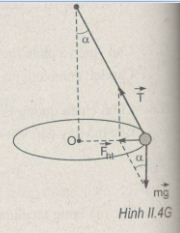
\(\tan \alpha = \displaystyle{{{F_{ht}}} \over P} = {{m{\omega ^2}r} \over {mg}} = {{{\omega ^2}l\sin \alpha } \over g}\)

\(\cos \alpha = \displaystyle{g \over {{\omega ^2}l}} = {{9,8} \over {{{(3,14)}^2}.1,00}} = 0,9940\)

\(\Rightarrow \alpha {\rm{ }} \approx {\rm{ }}{6^0}40'\)

b. Khi dây đứt, hòn đá chuyển động như một vật bị ném ngang với vận tốc 

v = ωr = ωlsin α = 3,14.1,00. 0,1167 = 0,366 m/s

Thời gian từ khi hòn đá bị văng ra đến khi chạm đất

\(t = \displaystyle \sqrt {{{2h} \over g}} = \sqrt {{{2.1,00} \over {9,8}}} = 0,452(s)\)

\(s = vt = 0,366.0,452 = 0,165 m = 16,5 cm\).

II.11.

Một viên đạn được bắn theo phương ngang từ một khẩu súng đặt ở độ cao 45 m so với mặt đất. Tốc độ của đạn lúc vừa ra khỏi nòng là 250 m/s. Lấy g = 9,8 m/s².

a) Đạn ở trong không khí bao lâu ?

b) Điểm đạn rơi xuống đất cách điểm bắn theo phương ngang bao xa ?

c) Khi rơi xuống đất, thành phần thẳng đứng của vận tốc của viên đạn có độ lớn bằng bao nhiêu ?

Phương pháp giải:

Sử dụng công thức:

- Công thức tính thời gian rơi \(t = \sqrt {\dfrac{{2h}}{g}} \)

- Công thức tính tầm xa \({L_{\max }} = {v_0}t\)

- Công thức tính vận tốc chạm đất \({v_y} = gt\)

Lời giải chi tiết:

a. \(t = \displaystyle \sqrt {{{2h} \over g}} = \sqrt {{{2.45} \over {9,8}}} = 3,03 \approx 3(s)\)

b. L_max = v₀t = 250.3,03 = 757,5 m.

c. v_y = gt = 9,8.3,03 = 29,7 ≈ 30 m/s.