Giải bài 9 trang 18 SGK Toán 10 tập 2 – Chân trời sáng tạo
Để quả bóng có thể ném được qua lưới cao 2 m, người ta phải đứng cách lưới bao xa? Làm tròn kết quả đến hàng phần mười
Đề bài
Quỹ đạo của một quả bóng được mô tả bằng hàm số \(y = f\left( x \right) = - 0,03{x^2} + 0,4x + 1,5\)
với y (tính bằng mét) là độ cao của quả bóng so với mặt đất khi độ dịch chuyển theo phương ngang của bóng là x (tính bằng mét). Để quả bóng có thể ném được qua lưới cao 2 m, người ta phải đứng cách lưới bao xa? Làm tròn kết quả đến hàng phần mười
Phương pháp giải - Xem chi tiết
Bước 1: Từ giả thiết lập bất phương trình
Bước 2: Giải bất phương trình vừa tìm được
Lời giải chi tiết
Để quả bóng có thể ném được qua lưới cao 2 m thì \(y = f\left( x \right) = - 0,03{x^2} + 0,4x + 1,5 > 2\)
\( \Rightarrow f\left( x \right) = - 0,03{x^2} + 0,4x - 0,5 > 0\)
Xét tam thức \(f\left( x \right) = - 0,03{x^2} + 0,4x - 0,5\) có \(\Delta = 0,1 > 0\), có hai nghiệm phân biệt là \({x_1} \simeq 1,4;{x_2} \simeq 11,9\) và có \(a = - 0,03 < 0\)
Ta có bảng xét dấu như sau
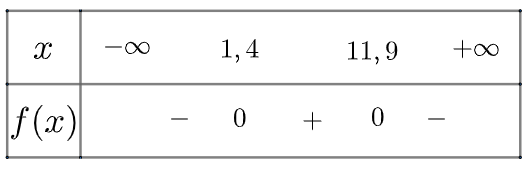
Vậy để quả bóng có thể ném được qua lưới cao 2 m, người ta phải đứng cách lưới từ 1,4 cho đến 11,9 mét
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 9 trang 18 SGK Toán 10 tập 2 – Chân trời sáng tạo timdapan.com"







