Bài 87 trang 90 SBT toán 8 tập 1

Đề bài

Cho hình bình hành \(ABCD\) có \(\widehat A = \alpha  > {90^0}.\) Ở phía ngoài hình bình hành, vẽ các tam giác đều \(ADF, ABE.\)

\(a)\) Tính \(\widehat {EAF}\)

\(b)\) Chứng minh rằng tam giác \(CEF\) là tam giác đều.

Lời giải chi tiết

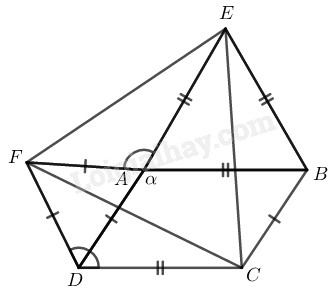
\(a)\) Vì \(\widehat {BAD} + \widehat {BAE} + \widehat {EAF} + \widehat {FAD} = {360^0}\)

\(\Rightarrow \widehat {EAF} = {360^0} - \left( {\widehat {BAD} + \widehat {BAE} + \widehat {FAD}} \right) \)

mà \(\widehat {BAD} = \alpha \) \((gt)\)

\(\widehat {BAE} = {60^0}\) (\(∆ BAE\) đều)

\(\widehat {FAD} = {60^0}\) (\(∆ FAD\) đều)

nên \(\widehat {EAF} = {360^0} - \left( {\alpha  + {{60}^0} + {{60}^0}} \right)\)\( = {240^0} - \alpha \)

\(b)\) Vì ABCD là hình bình hành nên \(AB//DC\)

Suy ra \(\widehat {ADC} + \widehat {BAD} = {180^0}\) (hai góc trong cùng phía bù nhau)

\(\Rightarrow \widehat {ADC} = {180^0} - \widehat {BAD} = {180^0} - \alpha\)

     \( \widehat {CDF} = \widehat {ADC} + \widehat {ADF} \)\(= {180^0} - \alpha  + {60^0} = {240^0} - \alpha \)

Suy ra: \(\widehat {CDF} = \widehat {EAF}\)

Tam giác ABE đều nên \(AE=AB=EB\)

Tam giác ADF đều nên \(AD=DF\)

Vì ABCD là hình bình hành nên \(AB=DC,AD=BC\)

Suy ra \(AE=EB = DC\) (vì cùng bằng \(AB\)) và \(BC = DF\) (vì cùng bằng \(AD\))

Xét \(∆ AEF\) và \(∆ DCF:\)

\(AF = DF\) (vì \(∆ ADF\) đều)

\(AE = DC\) (cmt)

\(\widehat {CDF} = \widehat {EAF}\) (chứng minh trên)

Do đó \(∆ AEF = ∆ DCF \;\;(c.g.c)\)

\(⇒ EF = CF \;\;(1)\)

\(\widehat {ADC} = \widehat {ABC}\) (tính chất hình bình hành)

\(\widehat {CBE} = \widehat {ABC} + {60^0} = \widehat {ADC} + {60^0}\)\( = {180^0} - \alpha  + {60^0} = {240^0} - \alpha \)

Xét \(∆ BCE\) và \(∆ DCF:\) 

\(BE = CD\) (cmt)

\(\widehat {CBE} = \widehat {CDF} = {240^0} - \alpha \)

\(BC = DF\) (cmt)

Do đó: \(∆ BCE = ∆ DFC\;\; (c.g.c)\)

\(⇒ CE = CF\;\; (2)\)

Từ \((1)\) và \((2)\) suy ra : \(EF = CF = CE.\) Vậy \(∆ ECF\) đều.