Bài 8 trang 72 Vở bài tập toán 8 tập 2

Đề bài

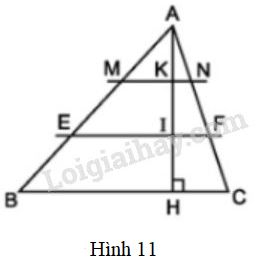
\(∆ABC\) có \(BC= 15cm\). Trên đường cao \(AH\) lấy các điểm \(I,K\) sao cho \(AK = KI = IH\). Qua \(I\) và \(K\) vẽ các đường \(EF // BC, MN // BC\) (h.11)

a) Tính độ dài đoạn thẳng \(MN\) và \(EF\).

b) Tính diện tích tứ giác \(MNFE\), biết diện tích của \(∆ABC\) là \(270\) cm²

Lời giải chi tiết

 a) Xét \(∆AEI\) có \(MK // EI\) do đó

\(\dfrac{{AM}}{{ME}} = \dfrac{{AK}}{{KI}} = 1 \Rightarrow AM = ME\)  (1)

Xét \(∆ABH\) có \(EI//BC\) do đó 

\(\dfrac{{AE}}{{AB}} = \dfrac{{AI}}{{AH}} = \dfrac{2}{3} \Rightarrow AE = \dfrac{2}{3}AB\)  (2)

Từ (1) và (2) suy ra \(AM=ME=EB\).

Theo hệ quả của định lí Ta - lét, ta có:

\(\dfrac{{MN}}{{BC}} = \dfrac{{AM}}{{AB}} = \dfrac{1}{3}\) \( \Rightarrow MN = \dfrac{1}{3}BC = \dfrac{1}{3}.15\left( {cm} \right) \)\(\,= 5\left( {cm} \right).\)

\(\dfrac{{EF}}{{BC}} = \dfrac{{AE}}{{AB}} = \dfrac{2}{3}\) \( \Rightarrow EF = \dfrac{2}{3}BC = \dfrac{2}{3}.15\left( {cm} \right) \)\(\,= 10\left( {cm} \right).\)

b) Áp dụng kết quả bài 7 ở trên ta có:

\(\dfrac{{{S_{AMN}}}}{{{S_{ABC}}}} = \dfrac{{MN.AK}}{{BC.AH}} \)\(\,= \dfrac{{MN}}{{BC}}.\dfrac{{AK}}{{AH}} = \dfrac{1}{3}.\dfrac{1}{3} = \dfrac{1}{9}\)

Suy ra \({S_{AMN}} = \dfrac{1}{9}{S_{ABC}}\)

Tương tự, suy ra: \({S_{AEF}} = \dfrac{4}{9}{S_{ABC}}\).

Do đó: \({S_{MNEF}} = {S_{AEF}} - {S_{AMN}}\)\(\, = \dfrac{4}{9}{S_{ABC}} - \dfrac{1}{9}{S_{ABC}} \)\(\,= \dfrac{1}{3}{S_{ABC}}\)

Với \({S_{ABC}} = 270c{m^2}\), ta có \({S_{MNEF}} = \dfrac{1}{3}.270 = 90\left( {c{m^2}} \right).\)