Giải bài 8 trang 57 sách bài tập toán 8 - Chân trời sáng tạo
Chứng minh rằng trong một tứ giác, tổng độ dài hai đường chéo lớn hơn nửa chu vi tứ giác đó.
Đề bài
Chứng minh rằng trong một tứ giác, tổng độ dài hai đường chéo lớn hơn nửa chu vi tứ giác đó.
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức về đường chéo trong tứ giác: Trong tứ giác, đường chéo là đoạn thẳng nối hai đỉnh đối nhau.
+ Sử dụng kiến thức về bất đẳng thức trong tam giác để chứng minh: Trong một tam giác, tổng độ dài hai cạnh tam giác lớn hơn độ dài cạnh còn lại.
Lời giải chi tiết
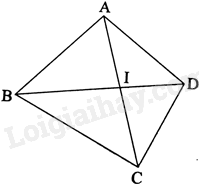
Vẽ tứ giác ABCD có I là giao điểm của hai đường chéo AC và BD.
Theo bất đẳng thức trong tam giác, ta có:
\(IA + IB > AB\), \(IB + IC > BC\), \(IC + ID > CB\), \(IA + ID > AD\)
Do đó: \(2\left( {IA + IB + IC + ID} \right) > AB + BC + CD + DA\)
Hay \(2\left( {AC + BD} \right) > AB + BC + CD + DA\)
Do đó: \(AC + BD > \frac{{AB + BC + CD + DA}}{2}\) (đpcm)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 8 trang 57 sách bài tập toán 8 - Chân trời sáng tạo timdapan.com"







