Bài 8 trang 136 Vở bài tập toán 9 tập 2

Đề bài

Một hình nón được đặt vào bên trong một hình lập phương như hình 72 (cạnh của hình lập phương bằng 1). Hãy tính:

a) Bán kính đáy của hình nón

b) Độ dài đường sinh 

Lời giải chi tiết

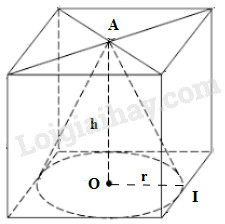
Gọi \(r\) là bán kính; \(l\) là đường sinh.

a) Ta có đáy hình nón nội tiếp của đáy hình lập phương cạnh bằng 1 \( \Rightarrow \) \(r = \dfrac{1}{2}.\)

b) Chiều cao hình lập phương \(h = AO = 1.\)

Xét tam giác \(OAI\) vuông tại \(O\), \(l = AI,r = OI.\) 

Ta có : \({l^2} = A{O^2} + O{I^2} = {1^2} + 0,{5^2}\)

Vậy \(l = \sqrt {{h^2} + {r^2}}  = \sqrt {{1^2} + 0,{5^2}}  = \dfrac{{\sqrt 5 }}{2}\)