Bài 13 trang 139 Vở bài tập toán 9 tập 2
Giải bài 13 trang 139 VBT toán 9 tập 2. Hãy điền đủ vào các ô trống (…) ở bảng sau...
Đề bài
Hãy điền đủ vào các ô trống (…) ở bảng sau:
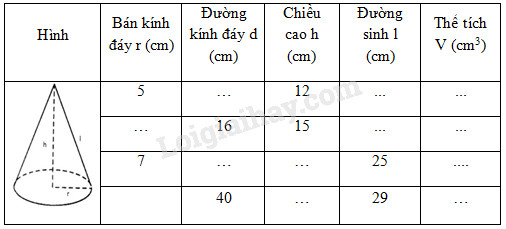
Phương pháp giải - Xem chi tiết
+ Đường kính đường tròn là \(d = 2r\)
+ Đường sinh hình nón \(l = \sqrt {{r^2} + {h^2}} \)
+ Thể tích hình nón bán kính đáy \(r\) và chiều cao \(h\) là \(V = \dfrac{1}{3}\pi {r^2}h\)
Lời giải chi tiết
+ Khi \(r = 5cm\) và \(h = 12cm,\) ta có \(d = 2r = 10\left( {cm} \right);\)
- Đường sinh \(l = \sqrt {{r^2} + {h^2}} = \sqrt {{5^2} + {{12}^2}} = 13\,\left( {cm} \right)\)
- Thể tích \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {.5^2}.12 = 100\pi\)\( \left( {c{m^3}} \right)\)
+ Khi \(d = 16cm\) và \(h = 15cm\), ta có \(r = 8\left( {cm} \right);\)
- Đường sinh \(l = \sqrt {{r^2} + {h^2}} = \sqrt {{8^2} + {{15}^2}} = 17\)\(\left( {\,cm} \right);\)
- Thể tích \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {.8^2}.15 = 320\pi\)\( \left( {c{m^3}} \right)\)
+ Khi \(r = 7cm\) và \(l = 25cm\) ta có \(d = 2r = 14\left( {cm} \right);\)
- Chiều cao \(h = \sqrt {{l^2} - {r^2}} = \sqrt {{{25}^2} - {7^2}} = 24\left( {cm} \right);\)
- Thể tích \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {.7^2}.24 = 392\pi\)\( \left( {c{m^3}} \right)\)
+ Khi \(d = 40cm\) và \(l = 29cm\), ta có \(r = 20\left( {cm} \right);\)
- Chiều cao \(h = \sqrt {{l^2} - {r^2}} = \sqrt {{{29}^2} - {{20}^2}} = 21\left( {cm} \right)\)
- Thể tích \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {.20^2}.21 = 2800\pi\)\( \left( {c{m^3}} \right)\).
Điền kết quả vào các ô trống trong bảng trên ta được bảng như sau :

Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 13 trang 139 Vở bài tập toán 9 tập 2 timdapan.com"







