Bài 12 trang 138 Vở bài tập toán 9 tập 2

Đề bài

Hình 75 cho ta hình ảnh của một cái đồng hồ cát với các kích thước kèm theo \((OA = OB)\). Hãy so sánh tổng thể tích của hai hình nón và thể tích hình trụ.

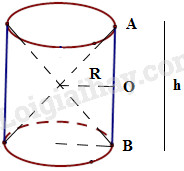
         Hình 75

Lời giải chi tiết

Gọi \({V_1},{V_2}\) là thể tích của hai hình nón;

\({h_1}\)  là chiều cao hình nón;

\({R_1}\) là bán kính hình nón.

Từ giả thiết ta có

\({V_1} = {V_2}\) vì \(OA = OB\); diện tích đáy bằng nhau

Suy ra \({V_n} =V_1+V_2=2V_1\) và \({R_1} = R;{h_1} = OA = OB = \dfrac{h}{2};\)

Theo công thức tính thể tích hình nón : \({V_n} = 2 \cdot \dfrac{1}{3}\pi {R^2} \cdot {h_1}\)

Do đó \({V_n} =2 \cdot \dfrac{1}{3}\pi {R^2}\dfrac{h}{2}= \dfrac{1}{3}\pi {R^2}{h}\)    (1)

Theo công thức tính thể tích hình trụ : \({V_T} = \pi {R^2}h.\)                 (2)

So sánh (1) và (2),  ta có  tổng thể tích hai hình nón bằng \( \dfrac{1}{3}\) thể tích hình trụ.