Giải bài 7.49 trang 37 sách bài tập toán 8 - Kết nối tri thức với cuộc sống
Chị Lan vay mẹ 900 nghìn đồng và dự định trả cho mẹ 100 nghìn đồng mỗi tuần.
Đề bài
Chị Lan vay mẹ 900 nghìn đồng và dự định trả cho mẹ 100 nghìn đồng mỗi tuần.
a) Viết công thức của hàm số biểu thị số tiền y (nghìn đồng) mà chị Lan còn nợ mẹ sau x (tuần) vay.
b) Vẽ đồ thị của hàm số thu được ở câu a. Từ đó tìm số tiền mà chị Lan nợ mẹ sau 4 tuần.
c) Giao điểm của đồ thị với trục hoành biểu thị điều gì?
Phương pháp giải - Xem chi tiết
a) Sử dụng khái niệm hàm số bậc nhất: Hàm số bậc nhất là hàm số cho bởi công thức \(y = ax + b,\) trong đó a, b là các số cho trước và \(a \ne 0\).
b) Sử dụng kiến thức về cách vẽ đồ thị hàm số bậc nhất \(y = ax + b\left( {a \ne 0} \right)\) để vẽ đồ thị
+ Khi \(b = 0\) thì \(y = ax\). Đồ thị của hàm số \(y = ax\) là đường thẳng đi qua gốc tọa độ O(0; 0) và điểm A(1; a)
+ Khi \(b \ne 0\), ta thường xác định hai điểm đặc biệt trên đồ thị là giao điểm của đồ thị với hai trục tọa độ như sau:
- Cho \(x = 0\) thì \(y = b\), ta được điểm P(0; b) thuộc trục tung Oy.
- Cho \(y = 0\) thì \(x = \frac{{ - b}}{a}\), ta được điểm \(Q\left( { - \frac{b}{a};0} \right)\) thuộc trục hoành Ox.
- Vẽ đường thẳng đi qua hai điểm P, Q ta được đồ thị của hàm số \(y = ax + b\)
Lời giải chi tiết
a) Số tiền chị Lan trả cho mẹ trong x tuần là: \(100x\) (nghìn đồng)
Công thức của hàm số biểu thị số tiền y (nghìn đồng) mà chị Lan còn nợ mẹ sau x (tuần) vay là: \(y = 900 - 100x\) (nghìn đồng)
b) Đồ thị hàm số: \(y = 900 - 100x\) (nghìn đồng) đi qua hai điểm B(0; 900) và G(9; 0)
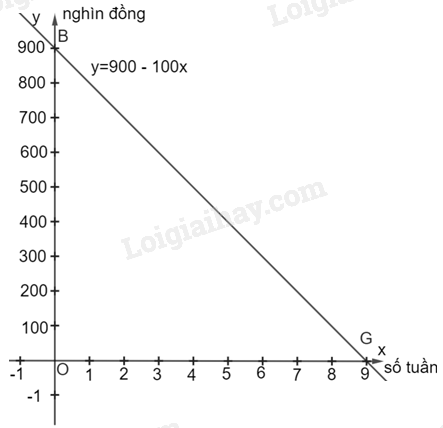
Với \(x = 4\) ta có: \(y = 900 - 100.4 = 500\) (nghìn đồng)
Vậy số tiền mà chị Lan nợ mẹ sau 4 tuần là 500 nghìn đồng.
c) Giao điểm của đồ thị hàm số \(y = 900 - 100x\) với trục hoành là điểm (9; 0). Giao điểm này biểu thị số tuần cần thiết để chị Lan trả hết nợ cho mẹ.
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 7.49 trang 37 sách bài tập toán 8 - Kết nối tri thức với cuộc sống timdapan.com"







