Bài 69 trang 50 SBT toán 7 tập 2
Giải bài 69 trang 50 sách bài tập toán 7. Cho tam giác ABC có Â là góc tù. Các đường trung trực của AB và của AC cắt nhau ở O và cắt BC theo thứ tự ở D và E...
Đề bài
Cho tam giác \(ABC\) có \(Â\) là góc tù. Các đường trung trực của \(AB\) và của \(AC\) cắt nhau ở \(O\) và cắt \(BC\) theo thứ tự ở \(D\) và \(E.\)
a) Các tam giác \(ABD, ACE\) là tam giác gì?
b) Đường tròn tâm \(O\) bán kính \(OA\) đi qua những điểm nào trong hình vẽ?
Phương pháp giải - Xem chi tiết
Sử dụng:
+) Ba đường trung trực của tam giác cùng đi qua một điểm. Điểm này cách đều ba đỉnh của tam giác đó.
+) Điểm thuộc đường trung trực của đoạn thẳng thì cách đều hai đầu mút của đường thẳng đó.
Lời giải chi tiết
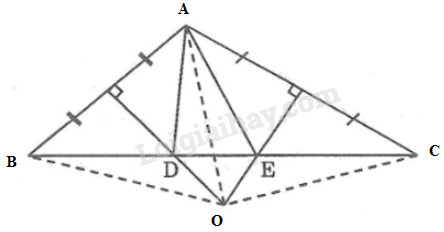
a) Vì \(D\) thuộc đường trung trực của \(AB\) nên \(DA = DB\) (tính chất đường trung trực)
Vậy \(∆ADB\) cân tại \(D.\)
Vì \(E\) thuộc đường trung trực của \(AC\) nên \(AE = EC\) (tính chất đường trung trực)
Vậy \(∆AEC\) cân tại \(E.\)
b) Vì \(O\) là giao điểm ba đường trung trực của \(∆ABC\) nên: \(OA = OB = OC\)
Vậy \((O;OA) \) đi qua ba điểm \(A, B, C.\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 69 trang 50 SBT toán 7 tập 2 timdapan.com"







