Giải bài 6.7 trang 16 SGK Toán 10 – Kết nối tri thức

Đề bài

Vẽ các đường parabol sau:

a) \(y = {x^2} - 3x + 2\) 

b) \(y =  - 2{x^2} + 2x + 3\)

c)\(y = {x^2} + 2x + 1\)   

d)\(y =  - {x^2} + x - 1\)

Lời giải chi tiết

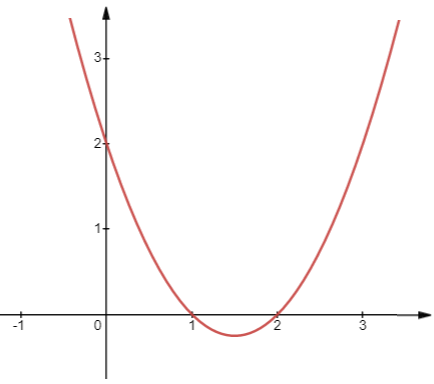
a) Đồ thị \(y = {x^2} - 3x + 2\)

- Có đỉnh là điểm \(I\left( {\frac{3}{2}; - \frac{1}{4}} \right)\), có trục đối xứng là đường thẳng \(x = \frac{3}{2}\)

- \(a = 1 > 0\), quay bề lõm lên trên

- Đi qua điểm (0;2);(1;0)

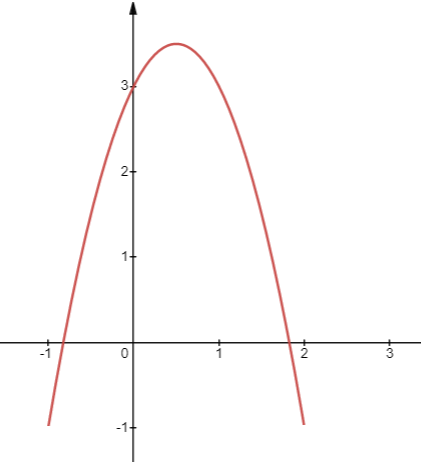
b) Đồ thị \(y =  - 2{x^2} + 2x + 3\)

- Có đỉnh là điểm \(I\left( {\frac{1}{2};\frac{7}{2}} \right)\), có trục đối xứng là đường thẳng \(x = \frac{1}{2}\)

- \(a =  - 2 < 0\), quay bề lõm xuống dưới

- Đi qua điểm (0;3);(1;3)

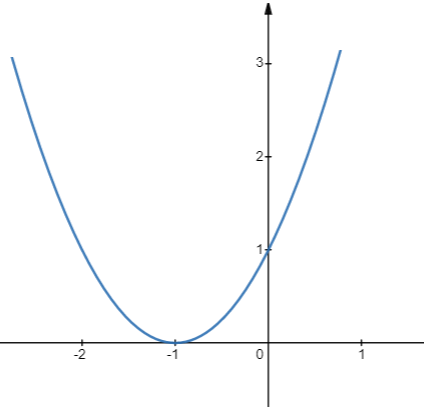
c) Đồ thị\(y = {x^2} + 2x + 1\)

- Có đỉnh là điểm \(I( - 1;0)\), có trục đối xứng là đường thẳng \(x =  - 1\)

- \(a = 2 > 0\), quay bề lõm lên trên

- Đi qua điểm (0;1); (1;4)

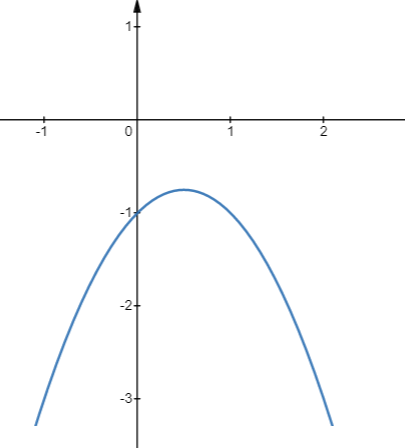
d) Đồ thị \(y =  - {x^2} + x - 1\)

- Có đỉnh là điểm \(I\left( {\frac{1}{2};\frac{{ - 3}}{4}} \right)\), có trục đối xứng là đường thẳng \(x = \frac{1}{2}\)

- \(a =  - 1 < 0\), quay bề lõm xuống dưới

- Đi qua điểm (0;-1);(1;-1)