Bài 6.3 phần bài tập bổ sung trang 165 SBT toán 8 tập 1

Đề bài

Bạn Giang đã vẽ một đa giác \(ABCDEFGHI\) như ở hình bs. 26.

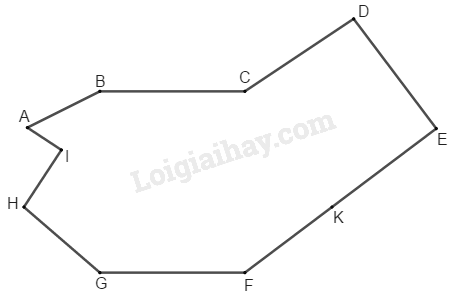
Tính diện tích của đa giác đó, biết rằng: \(KH\) song song với \(BC\) (\(K\) thuộc \(EF\)); \(BC\) song song với \(GF;\) \(CF\) song song với \(BG;\, BG\) vuông góc với \(GF;\, CK\) song song với \(DE;\, CD\) song song với \(FE;\, KE = DE\) và \(KE\) vuông góc với \(DE;\, I\) là trung điểm của \(BH,\, AI = IH\) và \(AI\) vuông góc với \(IH; HK = 11cm.\) \(HK\) cắt \(CF\) tại \(J\) và \(JK = 3 \,(cm),\) \(CJ = 4cm.\) \(BG\) cắt \(HK\) tại \(M\) và \(HM = 2cm.\)

Lời giải chi tiết

Chia đa giác đó thành hình vuông \(CDEK,\) hình thang \(KFGH,\) hình thang \(BCKH\) và tam giác vuông \(AIB\)

Ta có: \(MJ = KH – KJ – MH\) \(= 11 – 2 – 3 = 6\,(cm)\)

\(⇒ BC = GF = MJ = 6\, (cm)\)

\(CJ = 4 \,(cm)\)

\(\eqalign{ {S_{KFGH}} = {{HK + GF} \over 2}.FJ}\) \(= \eqalign{{11 + 6} \over 2}.2 = 17(c{m^2})\)

\(\eqalign{ {S_{BCKH}} = {{BC + KH} \over 2}.CJ}\) \(= \eqalign {{11 + 6} \over 2}.4 = 34(c{m^2}) \)

Trong tam giác vuông \(CJK\) có \(\widehat J = 90^\circ \). Theo định lý Pi-ta-go ta có:

\(C{K^2} = C{J^2} + J{K^2} = 16 + 9 = 25 \\\Rightarrow CK = 5\) \((cm)\)

\({S_{CDEK}} = C{K^2} = {5^2} = 25\) \((cm^2)\)

Trong tam giác vuông \(BMH\) có \(\widehat M = 90^\circ \). Theo định lý Pi-ta-go ta có:

\(B{H^2} = B{M^2} + H{M^2}\)

mà \(BM = CJ = 4\,(cm)\) (đường cao hình thang \(BCKH\))

\(\eqalign{  &  \Rightarrow B{H^2} = {4^2} + {2^2} = 20  }\) \(\Rightarrow \eqalign{IB = {{BH} \over 2} \Rightarrow I{B^2} = {{B{H^2}} \over 4}}\) \(\eqalign{= {{20} \over 4} = 5  }\)

Suy ra \({ IB = \sqrt 5 \,(cm) } \)

\(∆ AIB\) vuông cân tại \(I\) (vì \(AI = IH = IB\))

\({S_{AIB}} = \eqalign{1 \over 2}AI.IB = \eqalign{1 \over 2}I{B^2} = \eqalign{5 \over 2}\) \((cm^2)\)

\(S = {S_{CDEK}} + {S_{KFGH}} + {S_{BCKH}} \) \(+ {S_{AIB}} = 25 + 17 + 34 +\eqalign {5 \over 2} = \eqalign{{157} \over 2}\) \((cm^2)\)