Bài 51 trang 94 Vở bài tập toán 7 tập 2

Đề bài

Cho tam giác \(ABC\) vuông tại \(A\). Các đường trung trực của các cạnh \(AB, AC\) cắt nhau tại \(D\). Chứng minh rằng:

a) \(B, C, D\) thẳng hàng.

b) \(D\) là trung điểm của cạnh \(BC\).

Lời giải chi tiết

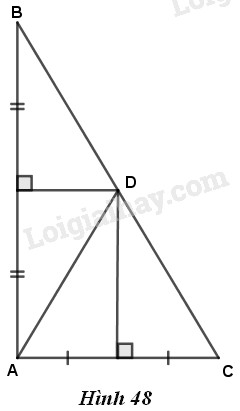
Để chứng minh ba điểm \(B,C,D\) thẳng hàng, ta sẽ chứng minh

\(\widehat {BDA} + \widehat {ADC} = 180^\circ \)

Ta có \(\widehat {BDA} = 180^\circ  - \left( {\widehat {ABD} + \widehat {BAD}} \right)\). Mặt khác, \(D\) thuộc đường trung trực của đoạn thẳng \(AB\) nên \(DB = DA\), hay tam giác \(DAB\) cân tại \(D\), suy ra \(\widehat B = \widehat {BAD}.\) Do đó

\(\widehat {BDA} = 180^\circ  - \left( {\widehat B + \widehat {BAD}} \right)\) \( = 180^\circ  - 2.\widehat {BAD}.\)           (1)

Tương tự, ta có

\(\widehat {ADC} = 180^\circ  - 2\widehat {DAC}\)         (2)

Từ (1) và (2) suy ra

\(\widehat {BDA} + \widehat {ADC} = \) \(360^\circ  - 2\left( {\widehat {BAD} + \widehat {DAC}} \right)\) \( = 360^\circ  - 2.90^\circ  = 180^\circ .\)

Vậy ba điểm \(B,D,C\) thẳng hàng.

b) Do các tam giác \(DAB\) và \(DAC\) cùng là tam giác cân nên \(BD = DA = DC\) (3)

Theo câu a, từ (3) suy ra \(D\) là trung điểm của cạnh \(BC.\)

Lưu ý: Bài này là bài toán tổng hợp của hai bài [55] và [56].