Giải bài 51 trang 29 sách bài tập toán 11 - Cánh diều
Giá trị của \(m\) để phương trình \(\cos x = m\) có nghiệm trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) là:
Đề bài
Giá trị của \(m\) để phương trình \(\cos x = m\) có nghiệm trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) là:
A. \(0 \le m < 1\)
B. \(0 \le m \le 1\)
C. \(0 < m \le 1\)
D. \(0 < m < 1\)
Phương pháp giải - Xem chi tiết
Sử dụng đồ thị hàm số \(y = \cos x\) để xác định giá trị của hàm trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\).
Lời giải chi tiết
Đồ thị hàm số \(y = \cos x\) trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) được vẽ như hình dưới đây.
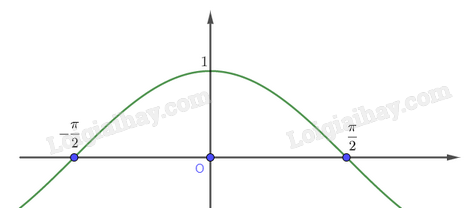
Nhìn vào đồ thị, ta thấy trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\), ta thấy \(0 < \cos x \le 1\).
Như vậy, để phương trình \(\cos x = m\) có nghiệm trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) thì \(0 < m \le 1\)
Đáp án đúng là C.
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 51 trang 29 sách bài tập toán 11 - Cánh diều timdapan.com"







