Giải bài 5 trang 91 vở thực hành Toán 8 tập 2
Cho các điểm A, B, C, D, E như Hình 9.30. Biết rằng \(\widehat{BAC}=\widehat{CDB}\). Chứng minh rằng ΔAED ∽ ΔBEC.
Đề bài
Cho các điểm A, B, C, D, E như Hình 9.30. Biết rằng \(\widehat{BAC}=\widehat{CDB}\). Chứng minh rằng ΔAED ∽ ΔBEC.
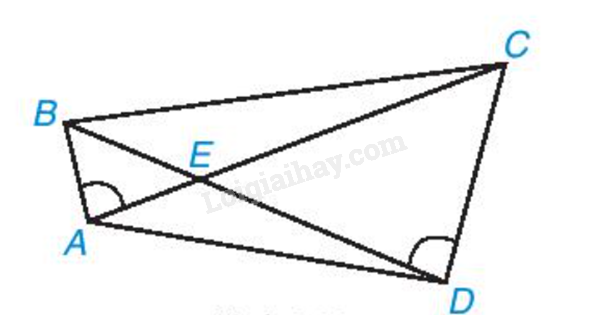
Phương pháp giải - Xem chi tiết
- Chứng minh ΔAEB ∽ ΔDEC suy ra: \(\frac{A\text{E}}{DE}=\frac{BE}{CE}\Rightarrow \frac{A\text{E}}{BE}=\frac{DE}{CF}\)
- Chứng minh ΔAED ∽ ΔBEC (c.g.c)
Lời giải chi tiết
Hai tam giác AEB và DEC có: $\widehat{AEB}=\widehat{DEC}$(hai góc đối đỉnh), $\widehat{BAC}=\widehat{CDB}$ (theo giả thiết).
Vậy $\Delta AEB\backsim \Delta DEC$ (g.g). Suy ra $\frac{EA}{ED}=\frac{EB}{EC}$, hay $\frac{EA}{EB}=\frac{ED}{EC}$.
Hai tam giác AED và BEC có: $\frac{EA}{EB}=\frac{ED}{EC}$ (theo chứng minh trên); $\widehat{AED}=\widehat{BEC}$ (hai góc đối đỉnh). Vậy ΔAED ∽ ΔBEC (c.g.c).
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 5 trang 91 vở thực hành Toán 8 tập 2 timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 5 trang 91 vở thực hành Toán 8 tập 2 timdapan.com"







