Giải bài 3 trang 90 vở thực hành Toán 8 tập 2
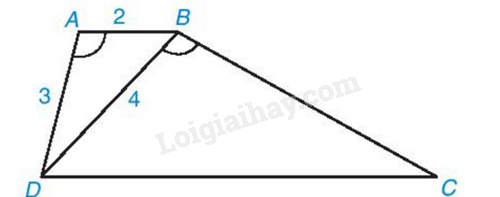
Cho hình thang ABCD (AB // CD) có \(\widehat{DAB}=\widehat{DBC}\)
Đề bài
Cho hình thang ABCD (AB // CD) có \(\widehat{DAB}=\widehat{DBC}\)
a) Chứng minh rằng ΔABD ∽ ΔBDC.
b) Giả sử AB = 2cm, AD = 3cm, BD = 4cm. Tính độ dài các cạnh BC và DC.
Phương pháp giải - Xem chi tiết
a) Chứng minh ΔABD ∽ ΔBDC (g.g)
b) Tính tỉ số đồng dạng của tam giác ABD và tam giác BDC. Từ đó tính độ dài của DC, BC
Lời giải chi tiết
a) Hai tam giác ABD và BDC có: $\widehat{ABD}=\widehat{BDC}$ (hai góc so le trong), $\widehat{DAB}=\widehat{CBD}$ (theo giả thiết).
Do đó $\Delta ABD\backsim \Delta BDC$ (g.g).
b) Từ $\Delta ABD\backsim \Delta BDC$ suy ra $\frac{AD}{BC}=\frac{BD}{DC}=\frac{AB}{BD}=\frac{1}{2}$.
Do đó BC = 2.AD = 6 (cm), DC = 2.BD = 8 (cm)
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 3 trang 90 vở thực hành Toán 8 tập 2 timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 3 trang 90 vở thực hành Toán 8 tập 2 timdapan.com"







