Giải Bài 5 trang 65 sách bài tập toán 7 - CTST
Cho hai đoạn thẳng AB và CD cắt nhau tại O. Tìm điểm M sao cho \(MA + MB + MC + M{\rm{D}}\) nhỏ nhất.
Đề bài
Cho hai đoạn thẳng AB và CD cắt nhau tại O. Tìm điểm M sao cho \(MA + MB + MC + M{\rm{D}}\) nhỏ nhất.
Phương pháp giải - Xem chi tiết
Sử dụng mối quan hệ giữa ba cạnh trong một tam giác.
Lời giải chi tiết
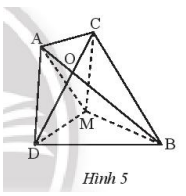
Ta có: \(MA + MB \ge AB,MC + M{\rm{D}} \ge C{\rm{D}}\)
Suy ra: \(MA + MB + MC + M{\rm{D}} \ge AB + C{\rm{D}}\)
MA + MB + MC + MD nhỏ nhất khi và chỉ khi \(MA + MB + MC + M{\rm{D = }}AB + C{\rm{D}}\)
Điều này xảy ra khi M trùng với điểm O.
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải Bài 5 trang 65 sách bài tập toán 7 - CTST timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải Bài 5 trang 65 sách bài tập toán 7 - CTST timdapan.com"







