Bài 48 trang 50 Vở bài tập toán 6 tập 2
Giải bài 48 trang 50 VBT toán 6 tập 2. Hoàn thành bảng nhân sau (chú ý rút gọn kết quả nếu có thể)...
Đề bài
Hoàn thành bảng nhân sau (chú ý rút ngắn gọn nếu có thể) :
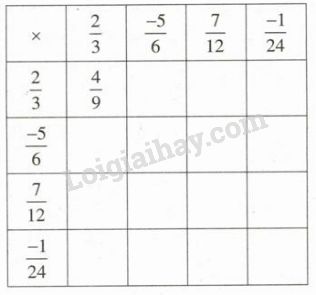
Phương pháp giải - Xem chi tiết
Muốn nhân hai phân số, ta nhân các tử với nhau và nhân các mẫu với nhau:
\(\dfrac{a}{b}.\dfrac{c}{d} = \dfrac{{a.c}}{{b.d}}\)
Lời giải chi tiết
Trước hết ta tính các kết quả ở “đường chéo chính” của hình vuông :
\(\begin{array}{l}\dfrac{{ - 5}}{6} \cdot \dfrac{{ - 5}}{6} = \dfrac{{\left( { - 5} \right).\left( { - 5} \right)}}{{6.6}} = \dfrac{{25}}{{36}};\\\dfrac{7}{{12}} \cdot \dfrac{7}{{12}} = \dfrac{{7.7}}{{12.12}} = \dfrac{{49}}{{144}};\\\dfrac{{ - 1}}{{24}} \cdot \dfrac{{ - 1}}{{24}} = \dfrac{{\left( { - 1} \right).\left( { - 1} \right)}}{{24.24}} = \dfrac{1}{{576}}\end{array}\)
Tiếp đó, ta tính các kết quả ở “đường chéo phụ” :
\(\begin{array}{l}\dfrac{{ - 5}}{6} \cdot \dfrac{2}{3} = \dfrac{{\left( { - 5} \right).2}}{{6.3}} = \dfrac{{\left( { - 5} \right).1}}{{3.3}}\\ = \dfrac{{ - 5}}{9};\\\dfrac{7}{{12}} \cdot \dfrac{{ - 5}}{6} = \dfrac{{7.\left( { - 5} \right)}}{{12.6}} = \dfrac{{ - 35}}{{72}};\\\dfrac{{ - 1}}{{24}} \cdot \dfrac{7}{{12}} = \dfrac{{\left( { - 1} \right).7}}{{24.12}} = \dfrac{{ - 7}}{{288}};\\\dfrac{7}{{12}} \cdot \dfrac{2}{3} = \dfrac{{7.2}}{{12.3}} = \dfrac{{7.1}}{{6.3}} = \dfrac{7}{{18}};\\\dfrac{{ - 1}}{{24}} \cdot \dfrac{{ - 5}}{6} = \dfrac{{\left( { - 1} \right).\left( { - 5} \right)}}{{24.6}} = \dfrac{5}{{144}};\\\dfrac{{ - 1}}{{24}} \cdot \dfrac{2}{3} = \dfrac{{\left( { - 1} \right).2}}{{24.3}} = \dfrac{{\left( { - 1} \right).1}}{{12.3}}\\ = \dfrac{{ - 1}}{{36}}.\end{array}\)
Do tính chất giao hoán của phép nhân phân số, ta có ngay các kết quả :
\(\begin{array}{l}\dfrac{2}{3} \cdot \dfrac{{ - 5}}{6} = \dfrac{{ - 5}}{6} \cdot \dfrac{2}{3} = \dfrac{{ - 5}}{9};\\\dfrac{{ - 5}}{6} \cdot \dfrac{7}{{12}} = \dfrac{7}{{12}} \cdot \dfrac{{ - 5}}{6} = \dfrac{{ - 35}}{{72}};\\\dfrac{7}{{12}} \cdot \dfrac{{ - 1}}{{24}} = \dfrac{{ - 1}}{{24}} \cdot \dfrac{7}{{12}} = \dfrac{{ - 7}}{{288}};\\\dfrac{2}{3} \cdot \dfrac{7}{{12}} = \dfrac{7}{{12}} \cdot \dfrac{2}{3} = \dfrac{7}{{18}};\\\dfrac{{ - 5}}{6} \cdot \dfrac{{ - 1}}{{24}} = \dfrac{{ - 1}}{{24}} \cdot \dfrac{{ - 5}}{6} = \dfrac{5}{{144}};\\\dfrac{{ - 1}}{{24}} \cdot \dfrac{2}{3} = \dfrac{{ - 1}}{{24}} \cdot \dfrac{2}{3} = \dfrac{{ - 1}}{{36}}.\end{array}\)
Ta điền các kết quả tìm được vào bảng đã cho.
Lưu ý
Các phân số được sắp xếp trong bảng ở dòng 1 theo thứ tự bằng các phân số sắp xếp ở cột 1, vì vậy có thể áp dụng tính chất giao hoán của phép nhân phân số.
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 48 trang 50 Vở bài tập toán 6 tập 2 timdapan.com"