Giải bài 4.53 trang 68 sách bài tập toán 10 - Kết nối tri thức với cuộc sống
Cho tam giác ABC có AB = 1,BC = 2
Đề bài
Cho tam giác \(ABC\) có \(AB = 1,\,\,BC = 2\) và \(\widehat {ABC} = {60^ \circ }.\) Tích vô hướng \(\overrightarrow {BC} .\overrightarrow {CA} \) bằng
A. \(\sqrt 3 \)
B. \( - \sqrt 3 \)
C. \(3\)
D. \( - 3\)
Phương pháp giải - Xem chi tiết
- Áp dụng định lý cosin để tính \(AC\): \(A{C^2} = A{B^2} + B{C^2} - 2AB.BC.\cos \widehat {ABC}\)
- Áp dụng định lý sin để tính góc \(\widehat {ACB}\): \(\frac{{AB}}{{\sin \widehat {ACB}}} = \frac{{AC}}{{\sin \widehat {ABC}}}\)
- Áp dụng công thức tính tích vô hướng của \(\overrightarrow {BC} .\overrightarrow {CA} \)
Lời giải chi tiết
Gọi \(D\) là điểm đối xứng với \(B\) qua \(C\)
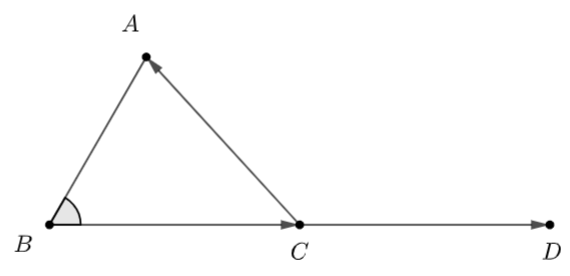
Áp dụng định lý cosin, ta có:
\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2AB.BC.\cos \widehat {ABC}\\ \Rightarrow \,\,A{C^2} = 1 + 4 - 2.1.2.\cos {60^ \circ } = 3\\ \Rightarrow \,\,AC = \sqrt 3 \end{array}\)
Áp dụng định lý sin, ta có:
\(\begin{array}{l}\frac{{AB}}{{\sin \widehat {ACB}}} = \frac{{AC}}{{\sin \widehat {ABC}}}\,\, \Leftrightarrow \,\,\frac{1}{{\sin \overrightarrow {ACB} }} = \frac{{\sqrt 3 }}{{\sin {{60}^ \circ }}}\\ \Leftrightarrow \,\,\sin \widehat {ACB} = \frac{{\sin {{60}^ \circ }}}{{\sqrt 3 }} = \frac{1}{2}\\ \Leftrightarrow \,\,\widehat {ACB} = {30^ \circ }\,\, \Rightarrow \,\,\widehat {ACD} = {180^ \circ } - {30^ \circ } = {150^ \circ }\end{array}\)
Ta có: \(\overrightarrow {BC} .\overrightarrow {CA} = \overrightarrow {CD} .\overrightarrow {CA} = CD.CA.\cos \left( {\overrightarrow {CD} ,\overrightarrow {CA} } \right) = 2.2.\cos {150^ \circ } = - 3\)
Chọn D.
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 4.53 trang 68 sách bài tập toán 10 - Kết nối tri thức với cuộc sống timdapan.com"







