Bài 4.12 trang 14 SBT Vật lí 7
Giải bài 4.12 trang 14 sách bài tập vật lí 7. Hai gương phẳng G1 và G2 có mặt phản xạ quay vào nhau và tạo với nhau một góc a (hình 4.9).
Đề bài
Hai gương phẳng \({G_1}\) và \({G_2}\) có mặt phản xạ quay vào nhau và tạo với nhau một góc \(\alpha\) (hình 4.9). Tia tới \(SI\) được chiếu lên gương Gi lần lượt phản xạ một lần trên gương \({G_1}\) rồi một lần trên gương \({G_2}\). Biết góc tới trên gương \({G_1}\) bằng \(30^0\). Tìm góc \(\alpha\) để cho tia tới trên gương \({G_1}\) và tia phản xạ trên gương \({G_2}\) vuông góc với nhau.
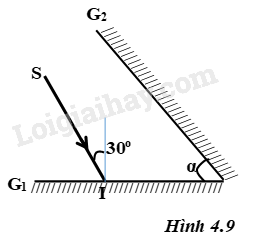
Phương pháp giải - Xem chi tiết
Sử dụng lí thuyết về định luật phản xạ ánh sáng: góc phản xạ bằng góc tới (\(i'=i\))
Lời giải chi tiết
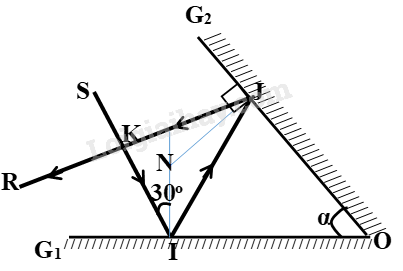
Tại \(I\), theo định luật phản xạ ánh sáng, ta có:
\(\widehat {SIN} = \widehat {NIJ} = {30^0}\)
\( \Rightarrow \widehat {JIO} = \widehat {NIO} - \widehat {NIJ} = {90^0} - {30^0} = {60^0}\)
Và \(\widehat {K{\rm{IJ}}} = {2.30^0} = {60^0}(1)\)
Trong \(\Delta IJO\), ta có:
\(\begin{array}{l}\widehat {{\rm{IJ}}O} = {180^0} - \widehat {JIO} - \widehat {IOJ}\\ = {180^0} - {60^0} - \alpha = {120^0} - \alpha \end{array}\)
\(\begin{array}{l} \Rightarrow \widehat {N{\rm{JI}}} = {90^0} - \widehat {{\rm{IJ}}O}\\ = {90^0} - ({120^0} - \alpha ) = \alpha - {30^0}\end{array}\)
Tại \(J\), theo định luật phản xạ ánh sáng, ta có:
\(\widehat {{\rm{IJ}}N} = \widehat {NJK}\)
\( \Rightarrow \widehat {KJI} = \widehat {IJN} + \widehat {NJK} = 2\widehat {IJN} = 2\alpha - {60^0}(2)\)
Từ (1) và (2) ta được:
\(\widehat {K{\rm{IJ}}} + \widehat {KJI} = {60^0} + 2\alpha - {60^0} = 2\alpha \)
Trong \(\Delta IKJ\), ta có:
\(\widehat {IKJ} = {180^0} - (\widehat {K{\rm{IJ}}} + \widehat {KJI}) = {180^0} - 2\alpha \)
Để tia tới \(SI\) trên gương \({G_1}\) vuông góc với tia phản xạ \(JR\) trên gương \({G_2}\) thì:
\(\begin{array}{l}\widehat {IKJ} = {90^0}\\ \Leftrightarrow {180^0} - 2\alpha = {90^0}\\ \Leftrightarrow \alpha = {45^0}\end{array}\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 4.12 trang 14 SBT Vật lí 7 timdapan.com"







