Bài 40 trang 100 Vở bài tập toán 8 tập 2

Đề bài

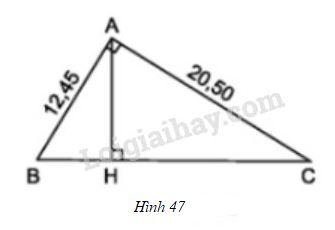
Ở hình 47, tam giác \(ABC\) vuông tại \(A\) có đường cao \(AH\)

a) Trong hình vẽ có bao nhiêu cặp tam giác đồng dạng? (Hãy chỉ rõ từng cặp tam giác đồng đạng và viết theo các đỉnh tương ứng). 

b) Cho biết: \(AB = 12,45 cm\), \(AC = 20,5cm\). Tính độ dài các đoạn thẳng \(BC, AH, BH\) và \(CH.\)

Lời giải chi tiết

a) Xét \(∆ABC \) và \( ∆HBA\) có:

\( \widehat{A} =  \widehat{H}={90^o}\)

\( \widehat{B}\) chung

\(\Rightarrow ∆ABC ∽ ∆HBA\) (g-g)

Xét \(∆ABC \) và \( ∆HAC\) có:

\( \widehat{A} = \widehat{H}={90^o}\)

\( \widehat{C}\) chung

\(\Rightarrow ∆ABC ∽ ∆HAC\) (g-g)

b) \(∆ABC\) vuông tại \(A\) (giả thiết) nên áp dụng định lí Pitago ta có:

\(\eqalign{
& B{C^2} = A{B^2} + A{C^2} \cr 
& \;\;\;\;\;\;\;\;= 12,{45^2} + 20,{50^2} = 575,2525 \cr 
& \Rightarrow BC = \sqrt {575,2525} \approx 24\,cm \cr} \)

\( ∆ABC ∽ ∆HBA \) (chứng minh trên)

\( \Rightarrow  \dfrac{AB}{HB} =  \dfrac{BC}{BA}\) 

\( \Rightarrow  HB =  \dfrac{AB^{2}}{BC} ≈  \dfrac{12,45^{2}}{24}≈ 6,5 cm\)

\( \Rightarrow CH = BC - BH \approx  24 - 6,5 \)\(\,= 17,5 cm.\)

Mặt khác: \( \dfrac{AC}{AH} =  \dfrac{BC}{BA}\)

\(\Rightarrow  AH = \dfrac{AB.AC}{BC}  \approx   \dfrac{12,45.20,50}{24}\)

\( \Rightarrow  AH  \approx  10,6 cm\).