Bài 39 trang 99 Vở bài tập toán 8 tập 2

Đề bài

Cho một tam giác vuông, trong đó có cạnh huyền dài \(20cm\) và một cạnh góc vuông dài \(12cm\). Tính độ dài hình chiếu cạnh góc vuông kia trên cạnh huyền.

Lời giải chi tiết

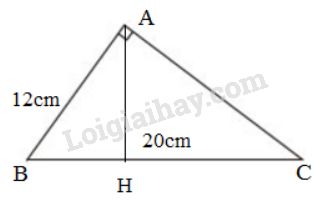
Giả sử tam giác \(ABC\) vuông tại \(A\) có cạnh huyền \(BC = 20cm\), cạnh góc vuông \(AB = 12cm\).

Hạ đường cao \(AH\), hình chiếu của \(AC\) trên cạnh huyền là \(HC\). Ta phải tính độ dài của \(HC\).

Xét hai tam giác vuông \(HBA\) và \(ABC\) có góc \(\widehat B\) chung

Do đó \(\Delta HBA \backsim \Delta ABC\).

Suy ra \(\dfrac{{HB}}{{AB}} = \dfrac{{BA}}{{BC}}\) \( \Rightarrow HB = \dfrac{{A{B^2}}}{{BC}} = \dfrac{{{{12}^2}}}{{20}}\) \( \Rightarrow HB = 7,2\left( {cm} \right)\)

Từ đó ta có \(HC = BC - HB \) \(= 20 - 7,2 = 12,8\left( {cm} \right)\).