Bài 37 trang 112 Vở bài tập toán 9 tập 2

Đề bài

Cho hình bình hành \(ABCD\). Đường tròn đi qua ba đỉnh \(A, B, C\) cắt đường thẳng \(CD\) tại \(P\) khác \(C\). Chứng minh \(AP = AD\).

Lời giải chi tiết

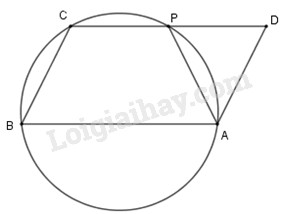
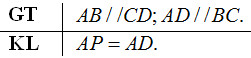
Từ \(AB//CD \Rightarrow \)\(\overparen{AP}=\overparen{CB}\) (vì hai cung bị chắn giữa hai dây song song thì bằng nhau), suy ra  \(AP = BC.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\)

Từ giả thiết ta có \(AD = BC\)                (2)

Vậy từ (1) và (2) \( \Rightarrow AP = AD.\)