Bài 36 trang 33 Vở bài tập toán 8 tập 2
Giải bài 36 trang 33 VBT toán 8 tập 2. Một ca nô xuôi dòng từ bến A đến bến B mất 4 giờ ...
Đề bài
Một ca nô xuôi dòng từ bến A đến bến B mất \(4\) giờ và ngược dòng từ bến B về bến A mất \(5\) giờ. Tính khoảng cách giữa hai bến A và B, biết rằng vận tốc của dòng nước là \(2 km/h\).
Phương pháp giải - Xem chi tiết
Áp dụng công thức của bài toán chuyển động trên dòng nước:
Vận tốc xuôi dòng = Vận tốc thực + vận tốc dòng nước.
Vận tốc ngược dòng = Vận tốc thực - vận tốc dòng nước.
Vận tốc xuôi dòng \(-\) vận tốc ngược dòng \(=\) vận tốc dòng nước \( \times 2\).
Bước 1: Gọi khoảng cách giữa A và B là ẩn, đặt điều kiện cho ẩn.
Bước 2: Biểu diễn các đại lượng khác qua ẩn
Bước 3: Lập phương trình thông qua các mối liên hệ giữa các đại lượng, giải phương trình
Bước 4: Kết luận
Lời giải chi tiết
Gọi \(x \,(km)\) là khoảng cách giữa hai bến A và B (điều kiện là \(x > 0\)). Ta lập bảng:
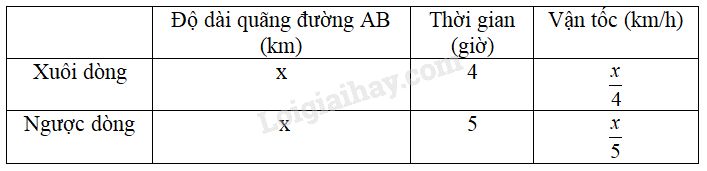
Hiệu vận tốc xuôi dòng và vận tốc ngược dòng bằng \(2\) lần vận tốc dòng nước, do đó:
\(\dfrac{x}{4} - \dfrac{x}{5} = 2.2\)
\( \Leftrightarrow \dfrac{{5.x}}{{20}} - \dfrac{{4.x}}{{20}} = \dfrac{{80}}{{20}}\)
\( \Leftrightarrow 5{\rm{x}} - 4{\rm{x}} = 80\)
\(\Leftrightarrow x = 80\) (thỏa mãn điều kiện).
Vậy khoảng cách giữa hai bến A và B là \(80 km\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 36 trang 33 Vở bài tập toán 8 tập 2 timdapan.com"







