Bài 33 trang 91 SBT toán 8 tập 2

Đề bài

Cho tam giác \(ABC\) và một điểm \(O\) nằm trong tam giác đó. Gọi \(P, Q, R\) lần lượt là trung điểm của các đoạn thẳng \(OA, OB, OC.\)

a) Chứng minh rằng tam giác \(PQR\) đồng dạng với tam giác \(ABC.\) 

b) Tính chu vi của tam giác \(PQR\), biết rằng tam giác \(ABC\) có chu vi \(p\) bằng \(543\,cm\).

Lời giải chi tiết

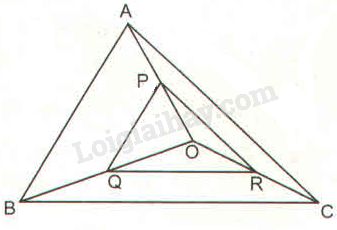
a) Xét \(\Delta AOB\) có:

\(P\) là trung điểm của \(OA\) (gt)

\(Q\) là trung điểm của \(OB\) (gt)

Do đó \( PQ\) là đường trung bình của \(∆ OAB.\)

\( \Rightarrow \displaystyle PQ = {1 \over 2}AB\) (tính chất đường trung bình của tam giác)

\( \Rightarrow \displaystyle {{PQ} \over {AB}} = {1 \over 2}\)                     (1)

Xét \(\Delta OAC\) có:

\(P\) là trung điểm của \(OA\) (gt)

\(R\) là trung điểm của \(OC\) (gt)

Do đó \(PR\) là đường trung bình của tam giác \(OAC.\)

\( \Rightarrow \displaystyle PR = {1 \over 2}AC\) (tính chất đường trung bình của tam giác )

\( \Rightarrow \displaystyle{{PR} \over {AC}} = {1 \over 2}\)                     (2)

Xét \(\Delta OBC\) có:

\(Q\) là trung điểm của \(OB\) (gt)

\(R\) là trung điểm của \(OC\) (gt)

Do đó \(QR\) là đường trung bình của tam giác \(OBC.\)

\( \Rightarrow \displaystyle QR = {1 \over 2}BC\)  (tính chất đường trung bình của tam giác )

\( \Rightarrow \displaystyle{{QR} \over {BC}} = {1 \over 2}\)                     (3)

Từ (1), (2) và (3) suy ra: \(\displaystyle  {{PQ} \over {AB}} = {{PR} \over {AC}} = {{QR} \over {BC}} = {1 \over 2}\)

Vậy \(∆ PQR\) đồng dạng \(∆ ABC \) (c.c.c).

b) Gọi \(p’\) là chu vi tam giác \(PQR.\)

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

\(\displaystyle {{PQ} \over {AB}} = {{PR} \over {AC}} = {{QR} \over {BC}}\)\(\,\displaystyle  = {{PQ + PR + QR} \over {AB + AC + BC}} = {{p'} \over p}=\dfrac{1}{2}\)

\(\displaystyle  \Rightarrow p' = {1 \over 2}p = {1 \over 2}.543 = 271,5\; (cm)\).