Giải bài 3.12 trang 56 SGK Toán 8 tập 1 - Kết nối tri thức
Cho M là một điểm nằm trong tam giác đều ABC.
Đề bài
Cho M là một điểm nằm trong tam giác đều ABC. Qua M kẻ các đường thẳng song song với BC, CA, AB lần lượt cắt AB, BC, CA tại các điểm P, Q, R.
a) Chứng minh tứ giác APMR là hình thang cân
b) Chứng minh rằng chu vi tam giác PQR bằng tổng độ dài MA + MB + MC.
c) Hỏi với vị trí nào của M thì tam giác PQR là tam giác đều?
Phương pháp giải - Xem chi tiết
a) Chứng minh: Tứ giác APMR là hình thang có \(\widehat {ABC} = \widehat {APM}\) nên tứ giác APMR là hình thang cân.
b) Chứng minh: AM = PR ; BM = PQ; MC = PQ nên PR + BM + QR = MA + MB + MC.
c) Vì điểm M cách đều ba đỉnh A, B, C của tam giác ABC do đó M là giao điểm của ba đường trung trực của tam giác ABC.
Lời giải chi tiết
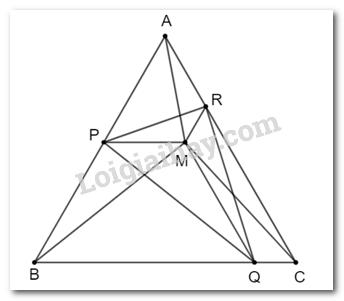
a) Vì tam giác ABC đều nên \(\widehat {BAC} = \widehat {ABC} = \widehat {ACB} = {60^o}\)
Vì PM // BC nên \(\widehat {ABC} = \widehat {APM} = {60^o}\)
Tứ giác APMR là hình thang (vì MR // AP) có \(\widehat {ABC} = \widehat {APM}\)
Do đó tứ giác APMR là hình thang cân.
b) Vì tứ giác APMR là hình thang cân nên AM = PR (1)
Vì MQ // AC nên \(\widehat {BQM} = \widehat {ACB} = {60^o}\)
Tứ giác BPMQ là hình thang (vì PM // BQ) có \(\widehat {BQM} = \widehat {ACB}\) nên BPMQ là hình thang cân.
Suy ra BM = PQ (2)
Chứng minh tương tự, ta có MC = QR (3)
Từ (1); (2) và (3) suy ra PR + BM + QR = MA + MB + MC.
Do đó chu vi tam giác PQR bằng tổng độ dài MA + MB + MC (đpcm).
c) Vì chu vi tam giác PQR bằng tổng độ dài MA + MB + MC
Để tam giác PQR là tam giác đều thì PQ = QR = PR suy ra MA = MB = MC
Khi đó điểm M cách đều ba đỉnh A, B, C của tam giác ABC.
Do đó M là giao điểm của ba đường trung trực (đồng thời M cũng là giao điểm của ba đường trung tuyến, ba đường cao, đường phân giác).
Vậy khi M là giao điểm của ba đường trung trực thì tam giác PQR là tam giác đều.
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 3.12 trang 56 SGK Toán 8 tập 1 - Kết nối tri thức timdapan.com"







