Giải bài 3.1 trang 50 SGK Toán 8 tập 1 - Kết nối tri thức
Tính góc chưa biết của các tứ giác trong Hình 3.8.
Đề bài
Tính góc chưa biết của các tứ giác trong Hình 3.8.
Phương pháp giải - Xem chi tiết
Áp dụng định lí tổng các góc trong một tứ giác bằng \(360^0\)
Lời giải chi tiết
• Hình 3.8a)
Xét tứ giác ABCD có:
\(\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\)
Hay 90°+90°+ˆC+90°=360°
Khi đó \(\widehat C\)+270°=360°
Do đó \(\widehat C\)=360°−270°=90°.
Vậy \(\widehat C\)=90°
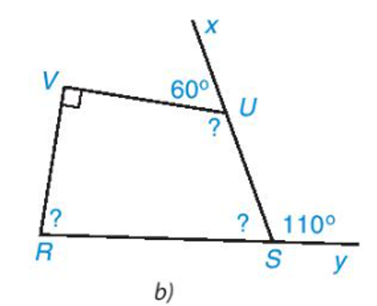
• Hình 3.8b)
Vì \(\widehat {{\rm{VUS}}}\) và \(\widehat {VUx}\) là hai góc kề bù nên ta có: \(\widehat {{\rm{VUS}}} + \widehat {VUx} = {180^o}\)
Hay \(\widehat {{\rm{VUS}}}\)+60°=180°
Suy ra \(\widehat {{\rm{VUS}}}\)=180°−60°=120°
Vì \(\widehat {US{\rm{R}}}\)và \(\widehat {USy}\)là hai góc kề bù nên ta có: \(\widehat {US{\rm{R}}} + \widehat {USy} = {180^o}\)
Hay \(\widehat {US{\rm{R}}}\)+110°=180o
Suy ra \(\widehat {US{\rm{R}}}\) =180°−110°=70°
Do đó \(\widehat {US{\rm{R}}}\)=70°
Xét tứ giác VUSR có:
\(\widehat V + \widehat {{\rm{VUS}}} + \widehat {V{\rm{SR}}} + \widehat R = {360^o}\)
Hay 90°+120°+70°+\(\widehat R\)=360°
Khi đó 280°+\(\widehat R\)=360°
Do đó \(\widehat R\)=360°−280°=80°
Vậy \(\widehat R\)=80°
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 3.1 trang 50 SGK Toán 8 tập 1 - Kết nối tri thức timdapan.com"