Bài 26 trang 89 SBT toán 8 tập 2
Giải bài 26 trang 89 sách bài tập toán 8. Tam giác ABC có AB = 3cm, BC = 5cm, CA = 7cm...
Đề bài
Tam giác \(ABC\) có \(AB = 3cm, BC = 5cm,\) \(CA = 7cm.\)
Tam giác \(A’B’C’\) đồng dạng với tam giác \(ABC\) có cạnh nhỏ nhất là \(4,5cm.\)
Tính các cạnh còn lại của tam giác \(A’B’C’.\)
Phương pháp giải - Xem chi tiết
Tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\) thì \(\displaystyle {{A'B'} \over {AB}} = {{A'C'} \over {AC}} = {{B'C'} \over {BC}} \).
Lời giải chi tiết
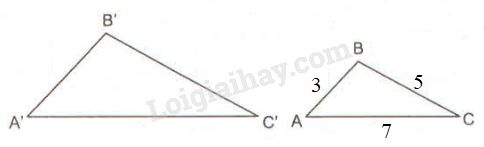
Tam giác \(A’B’C’\) đồng dạng với tam giác \(ABC\) có cạnh nhỏ nhất là \(4,5cm \) nên cạnh nhỏ nhất của \(∆ A’B’C’\) tương ứng với cạnh \(AB\) nhỏ nhất của \(∆ ABC.\)
Giả sử \(A’B’\) là cạnh nhỏ nhất của \(∆ A’B’C’\)
Vì \(∆ A’B’C’\) đồng dạng với tam giác \(ABC\) nên \(\displaystyle {{A'B'} \over {AB}} = {{A'C'} \over {AC}} = {{B'C'} \over {BC}}\) (1)
Thay \(AB = 3\;(cm), AC = 7 (cm),\) \(BC = 5 (cm) , A’B’ = 4,5 (cm)\) vào (1) ta được:
\(\displaystyle {{4,5} \over 3} = {{A'C'} \over 7} = {{B'C'} \over 5}\)
\( \Rightarrow \displaystyle A’C’ = {{7.4,5} \over 3} = 10,5\; (cm)\)
\( \Rightarrow \displaystyle B’C’ = {{5.4,5} \over 3} = 7,5\; (cm).\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 26 trang 89 SBT toán 8 tập 2 timdapan.com"







