Bài 26 trang 130 Vở bài tập toán 9 tập 1
Giải bài 26 trang 130 VBT toán 9 tập 1. Trên hình 86, tam giác ABC ngoại tiếp đường tròn (O)...
Đề bài
Trên hình \(86\), tam giác \(ABC\) ngoại tiếp đường tròn \((O)\).
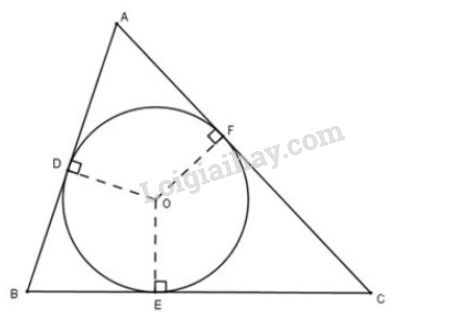
a) Chứng minh rằng:
\(2AD=AB+AC-BC.\)
b) Tìm các hệ thức tương tự hệ thức ở câu a).
Phương pháp giải - Xem chi tiết
Dùng tính chất hai tiếp tuyến cắt nhau tìm các cặp đoạn thẳng bằng nhau và biến đổi về phải sao cho kết quả bằng vế trái.
Lời giải chi tiết
a) Ta có \(AB = AD + BD,AC = AF + FC,\)\(BC = BE + EC\) nên
\(AB + AC - BC \)\(= \left( {AD + BD} \right) + \left( {AF + FC} \right) - \left( {BE + EC} \right)\)
\(=\left( {AD + AF} \right) + \left( {DB - BE} \right) + \left( {FC - EC} \right).\)
Theo tính chất của hai tiếp tuyến cắt nhau, ta có
\(DB = BE,FC = CE,AF = AD\)
Suy ra \(AB + AC - BC = AD + AF = 2AD.\)
Vậy \(2AD = AB + AC - BC.\)
b) Tương tự như hệ thức ở câu a), ta có :
\(2BE = BA + BC - CA\)
\(2CF = CA + CB - AB.\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 26 trang 130 Vở bài tập toán 9 tập 1 timdapan.com"







