Bài 24 trang 128 Vở bài tập toán 9 tập 1

Đề bài

Cho đường tròn (O), điểm I nằm bên ngoài đường tròn. Kẻ tiếp tuyến IA, IB với đường tròn (A, B là các tiếp điểm). Gọi H là giao điểm của IO và AB. Cho biết AB = 24cm, IA = 20cm.

a) Tính độ dài AH, IH, OH.

b) Tính bán kính của đường tròn (O). 

Lời giải chi tiết

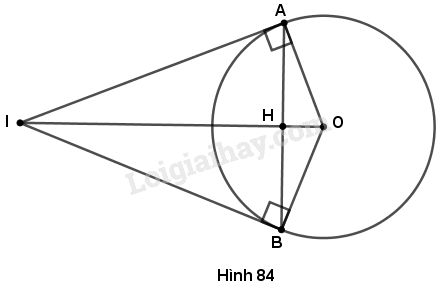
a) Theo tính chất của hai tiếp tuyến cắt nhau, ta có \(IA = IB,\) \(IO\) là tia phân giác của \(\widehat {AIB}\)

Tam giác  \(IAB\) cân tại \(I\) có \(IH\) là đường phân giác nên cũng là đường cao và đường trung tuyến.

Do đó \(AH = HB = \dfrac{{AB}}{2} = 12\left( {cm} \right).\)

Tính \(IH:\) Áp dụng định lí Py-ta-go vào tam giác vuông \(IAH\) ta có :

\(I{H^2} = A{I^2} - A{H^2}\)\( = {20^2} - {12^2} = 256\)

Suy ra \(IH = 16cm.\)

Tính \(OH:\) Xét tam giác \(OAI\) vuông tại \(A,\) đường cao \(AH,\) ta có :

\(A{H^2} = OH.IH\) hay \({12^2} = OH.16.\) Do đó \(OH = \dfrac{{{{12}^2}}}{{16}} = 9\left( {cm} \right).\)

b) Tính \(OA:\) Áp dụng định lí Py-ta-go vào tam giác vuông \(AHO\) ta có \(OA = \sqrt {A{H^2} + O{H^2}}  \)\(= \sqrt {{{12}^2} + {9^2}}  = \sqrt {225} \left( {cm} \right).\)

Do đó \(OA = 15cm.\)