Bài 25 trang 73 Vở bài tập toán 9 tập 1

Đề bài

a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của các hàm số sau

\(y = \dfrac{1}{2}x + 2;\,\,y =  - x + 2\)

b) Gọi giao điểm của hai đường thẳng \(y = \dfrac{1}{2}x + 2\) và \(y =  - x + 2\) với trục hoành theo thứ tự là A, B và gọi giao điểm của hai đường thẳng đó là C. Tính các góc của tam giác ABC (làm tròn đến độ).

c) Tính chu vi và diện tích của tam giác ABC (đơn vị đo trên các trục tọa độ là xentimet) 

Lời giải chi tiết

a) Đồ thị hàm số \(y = \dfrac{1}{2}x + 2\):

- Cho \(x = 0\) thì \(y = 2\) , ta được điểm \(C\left( {0;2} \right)\)

- Cho \(y=0\)  thì \(x =  - 4\) , được điểm \(A\left( { - 4;0} \right)\)

Vẽ đường thẳng đi qua hai điểm A và C, được đồ thì hàm số \(y = \dfrac{1}{2}x + 2\)

Đồ thị hàm số \(y =  - x + 2\)

- Cho \(x = 0\) thì \(y = 2\), được điểm \(C\left( {0;2} \right)\).

- Cho \(y = 0\) thì \(x = 2\), được điểm \(B\left( {2;0} \right)\)

Vẽ đường thẳng đi qua hai điểm B và C, được đồ thị của hàm số \(y =  - x + 2\).

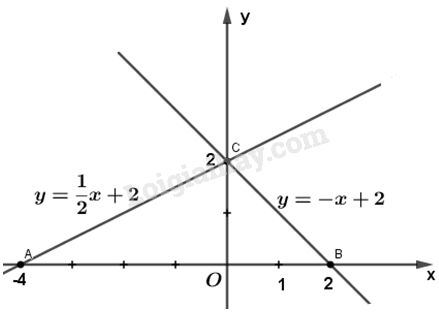
b) \({\mathop{\rm tanA}\nolimits}  = \dfrac{1}{2}\) \( \Rightarrow \widehat A \approx {27^o}\); \(\tan B = \left| { - 1} \right| \Rightarrow \widehat B = {45^o}\)

\(\widehat C = {180^o} - \left( {\widehat A + \widehat B} \right)\) \( \approx {180^o} - \left( {{{27}^o} + {{45}^o}} \right) = {108^o}\)

c) Gọi chu vi, diện tích tam giác ABC theo thứ tự là P, S. Áp dụng định lí Py-ta-go đối với các tam giác vuông OAC và OBC, ta tính được :

\(AC = \sqrt {O{A^2} + O{C^2}}  = \sqrt {{4^2} + {2^2}}  \)\(= \sqrt {20} \left( {cm} \right)\)

\(BC = \sqrt {O{B^2} + O{C^2}}  = \sqrt {{2^2} + {2^2}} \)\( = \sqrt 8 \left( {cm} \right)\)

\(AB = OA + OB = 4 + 2 = 6\left( {cm} \right)\)

Vậy \(P = AC + BC + AB = \sqrt {20}  + \sqrt 8  + 6\)\( \approx 13,3\left( {cm} \right)\)

\(S = \dfrac{1}{2}AB \cdot OC = \dfrac{1}{2} \cdot 6 \cdot 2 \)\(= 6\left( {c{m^2}} \right)\)