Bài 24 trang 159 SBT toán 8 tập 1
Giải bài 24 trang 159 sách bài tập toán 8. Chứng minh rằng tổng diện tích của hai hình vuông dựng trên hai cạnh góc vuông bằng diện tích của hình vuông dựng trên cạnh huyền.
Đề bài
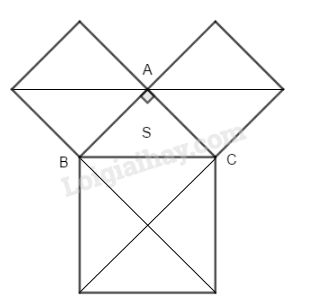
Cho một tam giác vuông cân. Chứng minh rằng tổng diện tích của hai hình vuông dựng trên hai cạnh góc vuông bằng diện tích của hình vuông dựng trên cạnh huyền (không sử dụng định lý Py-ta-go)
Phương pháp giải - Xem chi tiết
Chia các hình vuông thành các tam giác vuông cân rồi lập luận.
Lời giải chi tiết
Gọi \(S\) là diện tích của tam giác \(ABC\)
Hình vuông có cạnh \(AB\) được chia thành hai tam giác vuông cân bằng \(∆ ABC\) nên diện tích hình vuông cạnh \(AB\) bằng \(2S\)
Hình vuông có cạnh \(AC\) được chia thành hai tam giác vuông cân bằng \(∆ ABC\) nên có diện tích bằng \(2S\)
Hình vuông \(BC\) được chia thành \(4\) hình tam giác vuông cân bằng \(∆ ABC\) nên có diện tích bằng \(4S\)
Vì \(4S = 2S + 2S\) nên diện tích hình vuông dựng trên cạnh huyền bằng tổng diện tích hai hình vuông dựng trên hai cạnh góc vuông.
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 24 trang 159 SBT toán 8 tập 1 timdapan.com"