Bài 23 trang 87 SBT toán 6 tập 2
Giải bài 23 trang 87 sách bài tập toán 6. Trên đường thẳng d từ trái sang phải ta lấy các điểm A, D, C, B và lấy điểm O nằm ngoài đường thẳng d ....
Đề bài
Trên đường thẳng \(d\) từ trái sang phải ta lấy các điểm \(A, D, C, B\) và lấy điểm \(O\) nằm ngoài đường thẳng \(d\). Biết \(\widehat {AO{\rm{D}}} = {30^o},\widehat {DOC} = {40^o},\widehat {AOB} = {90^o}.\) Tính \(\widehat {AOC},\widehat {COB},\widehat {DOB}.\)
Phương pháp giải - Xem chi tiết
Áp dụng tính chất :
Nếu tia \(Oy\) nằm giữa tia \(Ox\) và tia \(Oz\) thì \(\widehat{xOy}+\widehat{yOz}=\widehat{xOz}\).
Lời giải chi tiết
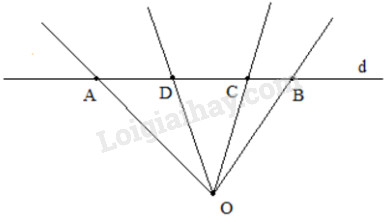
Vì \(D\) nằm giữa \(A\) và \(C\) nên tia \(OD\) nằm giữa hai tia \(OA\) và \(OC\), suy ra :
\(\widehat {AO{{D}}} + \widehat {DOC} = \widehat {AOC}\)
Thay \(\widehat {AO{{D}}} = {30^o};\widehat {DOC} = {40^o}\) ta có:
\(\widehat {AOC} = {30^o} + {40^o} = {70^o}\)
Vì \(C\) nằm giữa \(A\) và \(B\) nên tia \(OC\) nằm giữa hai tia \(OA\) và \(OB\), suy ra:
\(\widehat {AOC} + \widehat {COB} = \widehat {AOB}\)
Thay \(\widehat {AOC} = {70^o};\widehat {AOB} = {90^o}\) ta có:
\({70^o} + \widehat {COB} = {90^o}\)
\( \Rightarrow \widehat {COB} = {90^o} - {70^o} = {20^o}\)
Vì tia \(OD\) nằm giữa hai tia \(OA\) và \(OB\) nên:
\(\widehat {AO{{D}}} + \widehat {DOB} = \widehat {AOB}\)
Thay \(\widehat {AOD} = {30^o};\widehat {AOB} = {90^o}\) ta có:
\({30^o} + \widehat {DOB} = {90^o} \)
\(\Rightarrow \widehat {DOB} = {90^o} - {30^o} = {60^o}\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 23 trang 87 SBT toán 6 tập 2 timdapan.com"