Bài 18 trang 86 SBT toán 6 tập 2
Giải bài 18 trang 86 sách bài tập toán 6. Ở hình 6, hai tia OI, OK đối nhau. Tia OI cắt đoạn thẳng AB tại I...
Đề bài
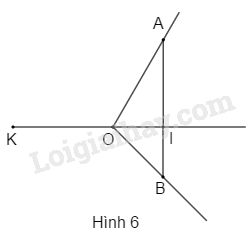
Ở hình 6, hai tia \(OI, OK\) đối nhau. Tia \(OI\) cắt đoạn thẳng \(AB\) tại \(I.\) Biết \(\widehat {K{\rm{O}}A} = {120^o},\widehat {BOI} = {45^o}\). Tính \(\widehat {K{\rm{O}}B},\widehat {AOI},\widehat {BOA}\).
Phương pháp giải - Xem chi tiết
Sử dụng:
- Tổng hai góc kề bù bằng \(180^o\).
- Nếu tia \(Oy\) nằm giữa tia \(Ox\) và tia \(Oz\) thì \(\widehat{xOy}+\widehat{yOz}=\widehat{xOz}\).
Lời giải chi tiết
Vì \(\widehat {K{\rm{O}}B}\) và \(\widehat {BOI}\) kề bù nên \(\widehat {K{\rm{O}}B} + \widehat {BOI} = {180^o}\)
Thay \(\widehat {BOI} = {45^o}\) ta được:
\(\widehat {K{\rm{O}}B} + {45^o} = {180^o}\)
\( \Rightarrow \) \(\widehat {K{\rm{O}}B} = {180^o} - {45^o} = {135^o}\)
Vì \(\widehat {K{\rm{OA}}}\) và \(\widehat {AOI}\) kề bù nên \(\widehat {K{\rm{O}}A} + \widehat {AOI} = {180^o}\)
Thay \(\widehat {K{\rm{O}}A} = {120^o}\) ta được:
\( {120^o}\widehat { + AOI} = {180^o} \)
\( \Rightarrow \widehat {AOI} = {180^o} - {120^o} = {60^o} \)
Vì tia \(OI\) nằm giữa hai tia \(OA\) và \(OB\) nên ta có:
\(\widehat {AOI} + \widehat {I{\rm{O}}B} = \widehat {AOB}\)
Thay \(\widehat {AOI} = {60^o};\widehat {I{\rm{O}}B} = {45^o}\) ta được:
\(\widehat {AOB} = {60^o} + {45^o} = {105^o}.\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 18 trang 86 SBT toán 6 tập 2 timdapan.com"







