Bài 2.1, 2.2 phần bài tập bổ sung trang 140 SBT toán 7 tập 1

Bài 2.1

Cho \(ΔABC = ΔDIK.\) \(\widehat B = {50^o},\widehat K = {40^o}\). Điền vào chỗ trống:

a) \(\widehat A=...\);

b) \(\widehat I=...\);

c) \(\widehat C=...\); 

Phương pháp giải:

- Định lí: Tổng ba góc của một tam giác bằng \({180^0}\).

- Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.

Lời giải chi tiết:

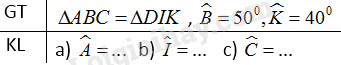
\(ΔABC =ΔDIK\) nên ta có:

\(\begin{array}{l}
\widehat A = \widehat D\\
\widehat B = \widehat I = {50^o}\\
\widehat C = \widehat K = {40^o}
\end{array}\)

Áp dụng định lí tổng các góc của một tam giác vào \(ΔABC \), ta có:

\(\begin{array}{l}
\widehat A + \widehat B + \widehat C = {180^o}\\
\Rightarrow \widehat A = {180^o} - \left( {\widehat B + \widehat C} \right)\\
\Rightarrow \widehat A = {180^o} - \left( {{{50}^o} + {{40}^o}} \right) \\\;\;\;\;\;\;\;\;\;= {180^o} - {90^o} = {90^o}
\end{array}\)

Ta điền như sau:

\(\begin{array}{l}
a)\,\widehat A = {90^o}\\ 
b)\,\widehat I = {50^o}\\
c)\,\widehat C = {40^o}
\end{array}\)

Bài 2.2

Cho \(ΔABC = ΔDEH.\) Biết \(AB = 5cm,\; AC = 6cm\), chu vi tam giác \(DEH\) bằng \(19cm.\) Tính độ dài các cạnh của tam giác \(DEH.\) 

Phương pháp giải:

- Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.

- Chu vi tam giác bằng tổng độ dài ba cạnh của tam giác đó.

Lời giải chi tiết:

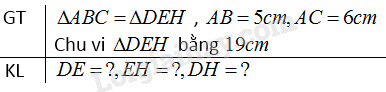
\(ΔABC = ΔDEH\) nên ta có: 

\(\begin{array}{l}
AB = DE = 5cm\\
BC = EH\\
AC = DH = 6cm
\end{array}\)

Chu vi tam giác \(DEH\) bằng \(19cm\) nên ta có:

\(\begin{array}{l}
DE + EH + DH = 19\\
\Rightarrow EH = 19 - \left( {DE + DH} \right)\\
\Rightarrow EH = 19 - \left( {5 + 6} \right) = 8\,\left( {cm} \right)
\end{array}\)

Vậy độ dài các cạnh của tam giác \(DEH\) là:

\(DE = 5cm,\; DH = 6cm, \;EH = 8cm.\)