Giải bài 2 trang 82 SGK Toán 8 – Cánh diều
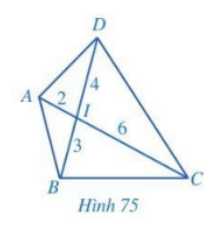
Cho Hình 75, chứng minh:
Đề bài
Cho Hình 75, chứng minh:
a) \(\Delta IAB \backsim \Delta IDC\)
b) \(\Delta IAD \backsim \Delta IBC\)
Phương pháp giải - Xem chi tiết
Tìm ra các tỉ số bằng nhau của các cạnh và chứng minh các cặp tam giác đồng dạng theo trường hợp đồng dạng thứ hai.
Lời giải chi tiết
a) Ta thấy \(\frac{{IA}}{{ID}} = \frac{2}{4} = \frac{1}{2};\,\,\frac{{IB}}{{IC}} = \frac{3}{6} = \frac{1}{2}\)
\( \Rightarrow \frac{{IA}}{{ID}} = \frac{{IB}}{{IC}}\)
Mà \(\widehat {AIB} = \widehat {DIC}\) (hai góc đối đỉnh)
Xét tam giác IAB và tam giác IDC có:
\(\frac{{IA}}{{ID}} = \frac{{IB}}{{IC}}\) và \(\widehat {AIB} = \widehat {DIC}\)
\( \Rightarrow \)\(\Delta IAB \backsim \Delta IDC\) (c-g-c)
b) Ta thấy \(\frac{{IA}}{{IB}} = \frac{2}{3};\,\,\frac{{ID}}{{IC}} = \frac{4}{6} = \frac{2}{3}\)
\( \Rightarrow \frac{{IA}}{{IB}} = \frac{{ID}}{{IC}}\)
Mà \(\widehat {AID} = \widehat {BIC}\) (hai góc đối đỉnh)
Xét tam giác IAD và tam giác IBC có:
\(\frac{{IA}}{{IB}} = \frac{{ID}}{{IC}}\) và \(\widehat {AID} = \widehat {BIC}\)
\( \Rightarrow \)\(\Delta IAD \backsim \Delta IBC\) (c-g-c)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 2 trang 82 SGK Toán 8 – Cánh diều timdapan.com"







