Bài 1.66 trang 38 SBT giải tích 12

Cho hàm số: \(y = \dfrac{{2x + 1}}{{x - 2}}\).

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.

b) Viết phương trình tiếp tuyến của đồ thị (C) , biết hệ số góc của tiếp tuyến bằng \( - 5\).

(Đề thi tốt nghiệp THPT năm 2009)

LG a

Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho

Phương pháp giải:

- Tìm TXĐ.

- Xét sự biến thiên.

- Vẽ đồ thị hàm số.

Lời giải chi tiết:

TXĐ: \(D = \mathbb{R}\backslash \left\{ 2 \right\}\).

Có \(y' = \dfrac{{ - 5}}{{{{\left( {x - 2} \right)}^2}}} < 0,\forall x \in D\) nên hàm số nghịch biến trên các khoảng \(\left( { - \infty ;2} \right)\) và \(\left( {2; + \infty } \right)\).

Giới hạn: \(\mathop {\lim }\limits_{x \to  \pm \infty } y = 2\) nên TCN \(y = 2\).

\(\mathop {\lim }\limits_{x \to {2^ + }} y =  + \infty ,\mathop {\lim }\limits_{x \to {2^ - }} y =  - \infty \) nên TCĐ \(x = 2\).

Bảng biến thiên:

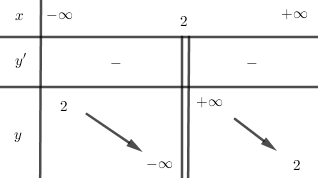
Đồ thị:

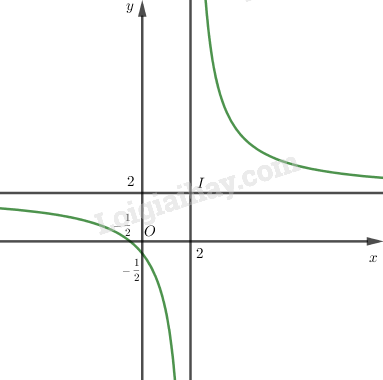
LG b

Viết phương trình tiếp tuyến của đồ thị (C) , biết hệ số góc của tiếp tuyến bằng \( - 5\).

Phương pháp giải:

- Giải phương trình \(y' = k\) tìm hoành độ giao điểm.

- Viết phương trình tiếp tuyến theo công thức \(y = k\left( {x - {x_0}} \right) + {y_0}\).

Lời giải chi tiết:

Ta có: \(y' = \dfrac{{ - 5}}{{{{\left( {x - 2} \right)}^2}}} =  - 5\)\( \Leftrightarrow {(x - 2)^2} = 1\) \( \Leftrightarrow \left[ \begin{array}{l}x - 2 = 1\\x - 2 =  - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 1\end{array} \right.\)

Với \(x = 3\) ta có \(y = 7\) nên phương trình tiếp tuyến là \(y =  - 5\left( {x - 3} \right) + 7\) hay \(y =  - 5x + 22\).

Với \(x = 1\) ta có \(y =  - 3\) nên phương trình tiếp tuyến là \(y =  - 5\left( {x - 1} \right) - 3\) hay \(y =  - 5x + 2\).