Bài 1.49 trang 24 SBT giải tích 12

Đề bài

a) Cho hàm số  \(y = \dfrac{{3 - x}}{{x + 1}}\)  có đồ thị \(\left( H \right).\)

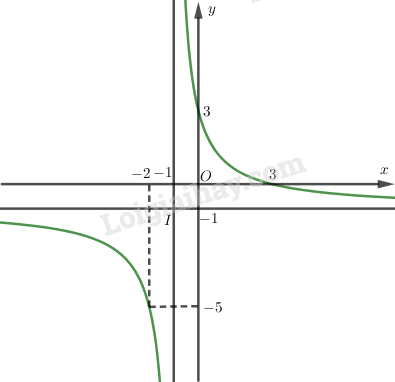
Chỉ ra một phép biến hình biến (H) thành (H’) có tiệm cận ngang \(y = 2\) và tiệm cận đứng \(x = 2\).

b) Lấy đối xứng (H’) qua gốc (O), ta được hình (H’’). Viết phương trình của (H’’).

Lời giải chi tiết

a) Từ đồ thị hàm số (H), để có hình (H’) nhận \(y = 2\) là tiệm cận ngang và \(x = 2\) là tiệm cận đứng, ta tịnh tiến đồ thị (H) song song với trục \(Oy\) lên trên \(3\) đơn vị, sau đó tịnh tiến song song với trục \(Ox\) về bên phải \(3\) đơn vị, ta được các hàm số tương ứng sau:

+ Tịnh tiến lên trên \(3\) đơn vị ta được: \(y = f(x) = \dfrac{{3 - x}}{{x + 1}} + 3\) \( = \dfrac{{3 - x + 3x + 3}}{{x + 1}} = \dfrac{{2x + 6}}{{x + 1}}\);

+ Tịnh tiến sang phải \(3\) đơn vị ta được: \(y = g(x) = \dfrac{{2(x - 3) + 6}}{{x - 3 + 1}} = \dfrac{{2x}}{{x - 2}}\,\,\left( {H'} \right)\)

b) Lấy đối xứng hình (H’) qua gốc O, ta được hình (H’’).

Lấy điểm M'(x;y) thuộc (H'), khi đó M'' là ảnh qua M qua phép đối xứng tâm O nên 

\(\left\{ \begin{array}{l}
{x_{M''}} = - x\\
{y_{M''}} = - y
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
x = - {x_{M''}}\\
y = - {y_{M''}}
\end{array} \right. \)

\(\Rightarrow M\left( { - {x_{M''}}; - {y_{M''}}} \right)\)

\(M\in (H')\) nên

\( - {y_{M''}} = \frac{{2\left( { - {x_{M''}}} \right)}}{{ - {x_{M''}} - 2}}\) \( \Leftrightarrow  - {y_{M''}} = \frac{{ - 2{x_{M''}}}}{{ - \left( {{x_{M''}} + 2} \right)}} \) \(\Leftrightarrow  - {y_{M''}} = \frac{{2{x_{M''}}}}{{{x_{M''}} + 2}}\) \(  \Leftrightarrow {y_{M''}} =  - \frac{{2{x_{M''}}}}{{{x_{M''}} + 2}}\)

Vậy M'' thuộc đồ thị hàm số (H'') \(y   = - \dfrac{{2x}}{{x + 2}}\)