Giải bài 13 trang 121 SGK Toán 8 tập 1 - Cánh diều

Đề bài

Cho hình vuông ABCD có M, N lần lượt là trung điểm của các cạnh BC, Cd. Gọi O là gao điểm của AM và BN. Chứng minh:

a) \(\Delta ABM = \Delta BCN\)

b) \(\widehat {BAO} = \widehat {MBO}\)

c) \(AM \bot BN\)

Lời giải chi tiết

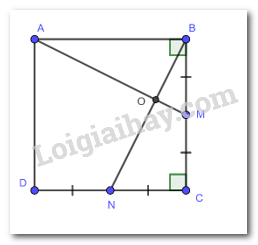
a) Vì ANCD là hình vuông

suy ra: AB = BC = CD = DA

Gọi M là trung điểm của các cạnh BC, CD

Suy ra: BM = MC = CN = CD

Xét hai tam giác vuông ABM và BCN có:

AB = BC

BM = CN

\( \Rightarrow \Delta ABM = \Delta BCN\) (hai cạnh góc vuông)

b) theo câu a: \(\Delta ABM = \Delta BCN\)

\(\begin{array}{l} \Rightarrow \widehat {BAM} = \widehat {CBN}\\ \Rightarrow \widehat {BAO} = \widehat {MBO}\end{array}\)

c) Vì \(\Delta ABM = \Delta BCN\)

\(\begin{array}{l} \Rightarrow \widehat {MAB} = \widehat {NBM}\\ \Rightarrow \widehat {MAB} = \widehat {OBM}\end{array}\)

Mà: \(\widehat {MAB} + \widehat {{M_1}} = {90^o}\) (do tam giác ABM vuông tại M)

\( \Rightarrow \widehat {OBM} + \widehat {{M_1}} = {90^o}\)

Xét tam giác OBM có:

\(\begin{array}{l}\widehat {BOM} + \widehat {OBM} + \widehat {{M_1}} = {180^o}\\ \Rightarrow \widehat {BOM} + {90^o} = {180^o}\\ \Rightarrow \widehat {BOM} = {180^o} - {90^o} = {90^o}\end{array}\)

Suy ra: tam giác OBM vuông tại O

\(\begin{array}{l} \Rightarrow BO \bot OM\\ \Rightarrow BN \bot AM\end{array}\)